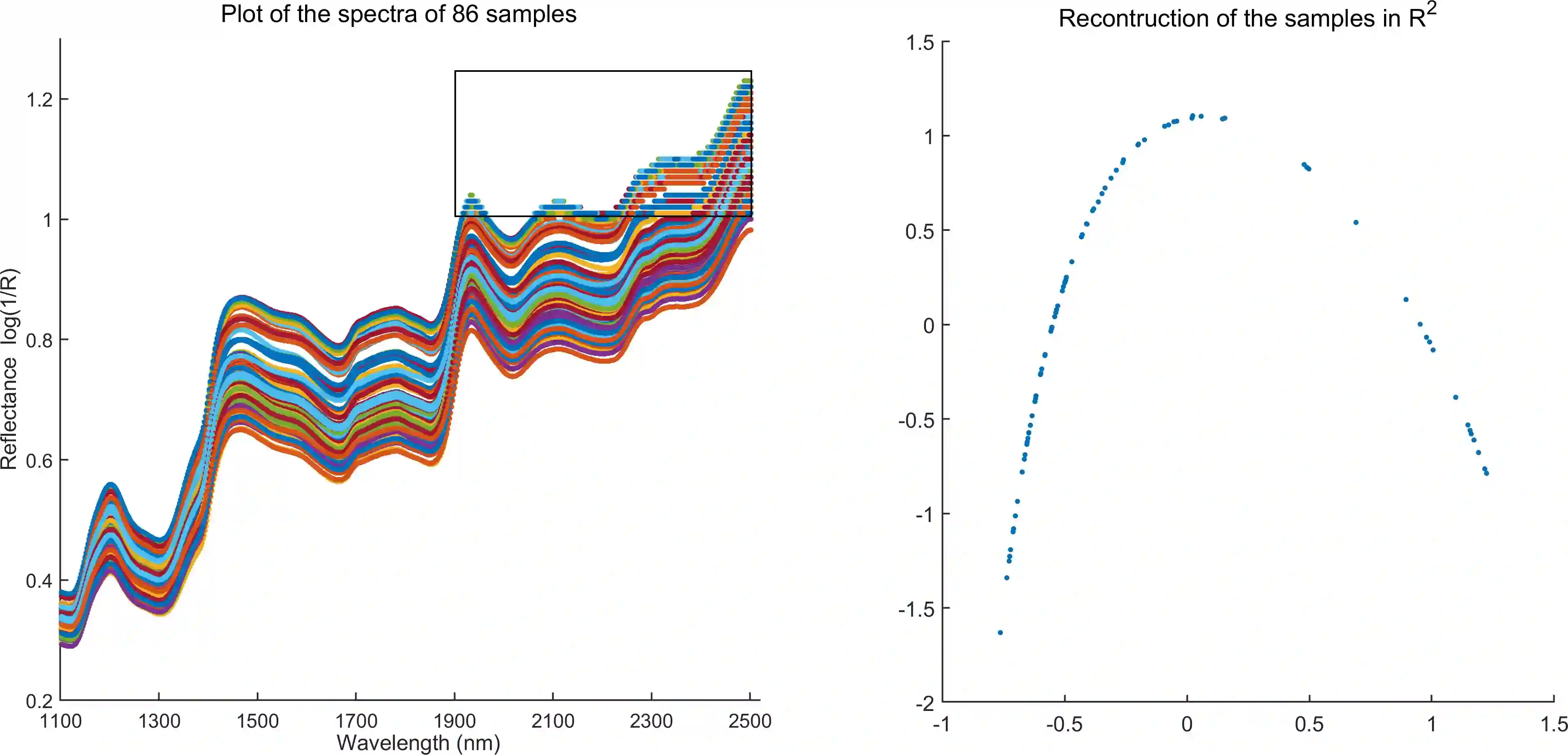
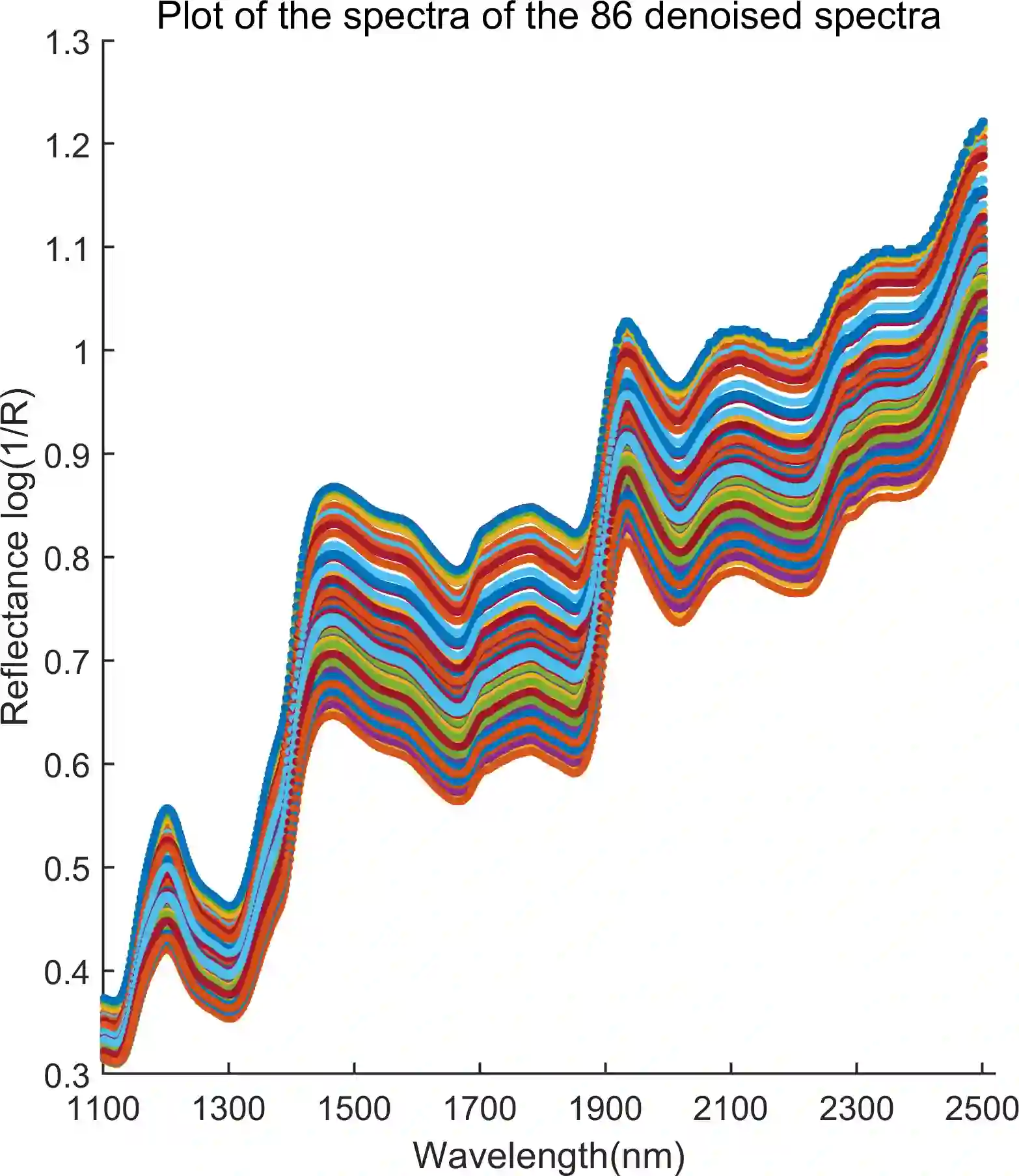
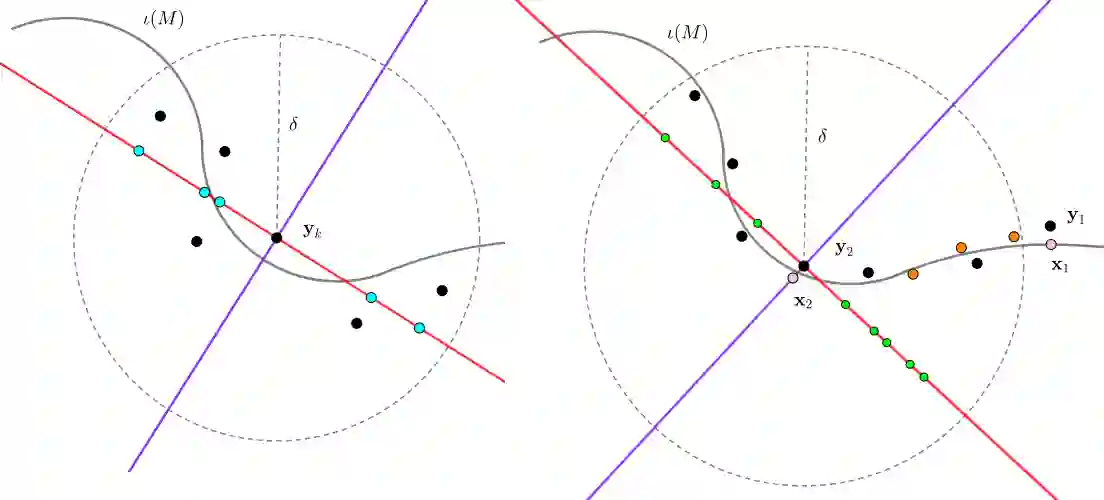
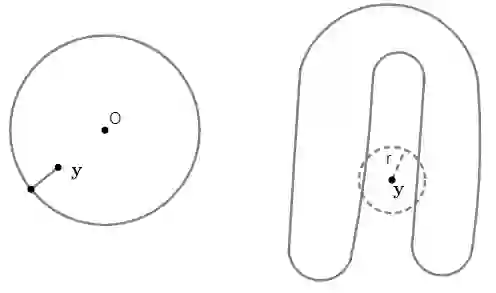
In analyzing complex datasets, it is often of interest to infer lower dimensional structure underlying the higher dimensional observations. As a flexible class of nonlinear structures, it is common to focus on Riemannian manifolds. Most existing manifold learning algorithms replace the original data with lower dimensional coordinates without providing an estimate of the manifold in the observation space or using the manifold to denoise the original data. This article proposes a new methodology for addressing these problems, allowing interpolation of the estimated manifold between fitted data points. The proposed approach is motivated by novel theoretical properties of local covariance matrices constructed from noisy samples on a manifold. Our results enable us to turn a global manifold reconstruction problem into a local regression problem, allowing application of Gaussian processes for probabilistic manifold reconstruction. In addition to theory justifying the algorithm, we provide simulated and real data examples to illustrate the performance.
翻译:在分析复杂的数据集时,通常有兴趣推断出高维观测背后的低维结构。作为一个灵活的非线性结构类别,关注里伊曼式的方块是常见的。大多数现有的多重学习算法以低维坐标取代原始数据,而没有提供对观测空间中的方块的估计,也没有使用方块来掩盖原始数据。本篇文章提出了解决这些问题的新方法,允许对安装数据点之间的估计方块进行内插。拟议方法的动机是,从从一个多维体上制造的噪音样品中制造的本地共变矩阵的新的理论性能。我们的结果使我们能够将一个全球多重重建问题变成一个局部回归问题,允许应用高森进程进行概率多维重建。除了为算法提供理论依据外,我们还提供了模拟和真实的数据示例,以说明其性能。