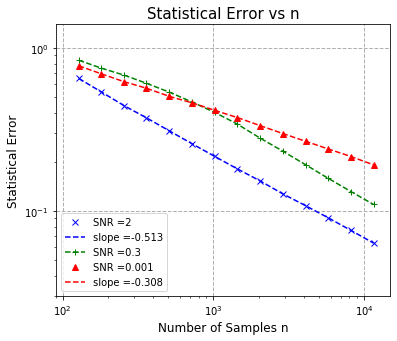
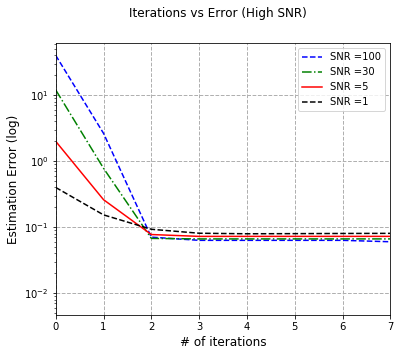
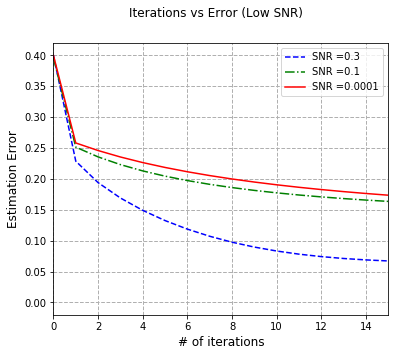
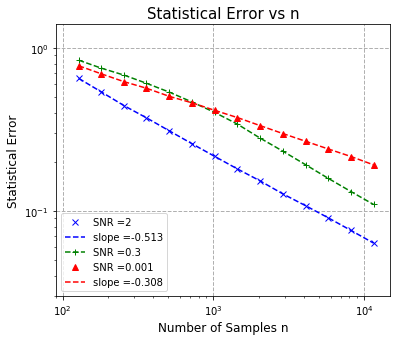
We study the convergence rates of the EM algorithm for learning two-component mixed linear regression under all regimes of signal-to-noise ratio (SNR). We resolve a long-standing question that many recent results have attempted to tackle: we completely characterize the convergence behavior of EM, and show that the EM algorithm achieves minimax optimal sample complexity under all SNR regimes. In particular, when the SNR is sufficiently large, the EM updates converge to the true parameter $\theta^{*}$ at the standard parametric convergence rate $\mathcal{O}((d/n)^{1/2})$ after $\mathcal{O}(\log(n/d))$ iterations. In the regime where the SNR is above $\mathcal{O}((d/n)^{1/4})$ and below some constant, the EM iterates converge to a $\mathcal{O}({\rm SNR}^{-1} (d/n)^{1/2})$ neighborhood of the true parameter, when the number of iterations is of the order $\mathcal{O}({\rm SNR}^{-2} \log(n/d))$. In the low SNR regime where the SNR is below $\mathcal{O}((d/n)^{1/4})$, we show that EM converges to a $\mathcal{O}((d/n)^{1/4})$ neighborhood of the true parameters, after $\mathcal{O}((n/d)^{1/2})$ iterations. Notably, these results are achieved under mild conditions of either random initialization or an efficiently computable local initialization. By providing tight convergence guarantees of the EM algorithm in middle-to-low SNR regimes, we fill the remaining gap in the literature, and significantly, reveal that in low SNR, EM changes rate, matching the $n^{-1/4}$ rate of the MLE, a behavior that previous work had been unable to show.
翻译:我们研究EM运算法的趋同率,以学习所有信号对噪音比率(SNR)的所有制度下的双成份混合线性回归。我们解决了一个长期存在的问题,许多最近的结果都试图解决这个问题:我们完全描述EM的趋同行为,并表明EM算法在所有SNR制度下达到最小最大样本复杂性。特别是,当SNR足够大时,EM更新会与真正的参数$(theta$)相融合,标准参数为$(mathcal{O}(d/n)%%1}(o}(d/n)%1/2}(r)) 标准准趋同率($) 。当SNRR超过$(m) (d)%1) 和低于常数的系统中,EM(d) 美元(r=%1) 和(d) 美元(r=(r) 数(d) 最低(nRRQ) 的初始变现率(nRR) 或(nR) 最低变数时,EM1 (d) 的变数(r=(r=) 美元) 最低变。