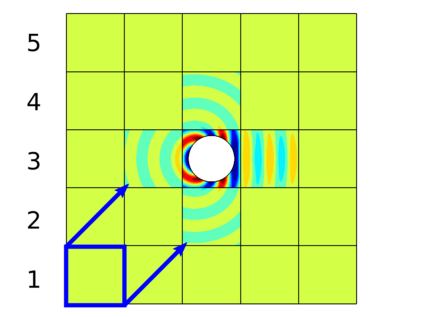
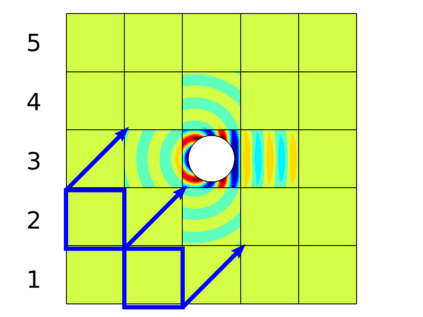
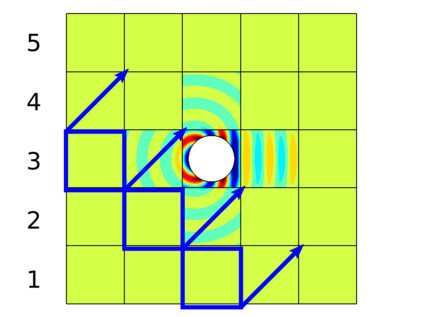
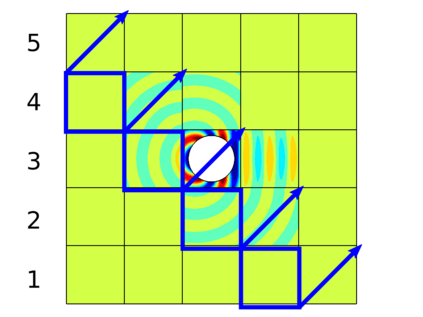
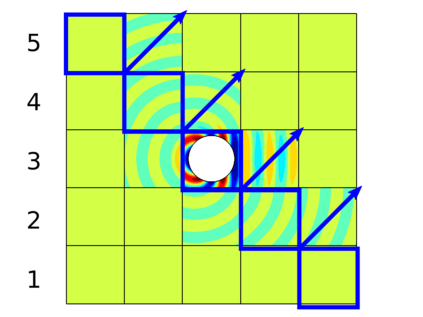
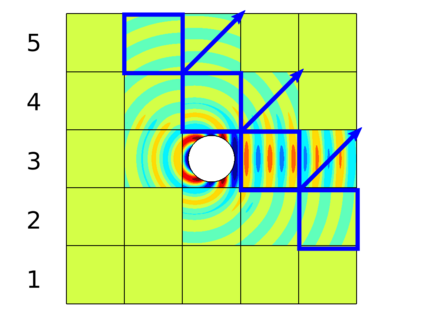
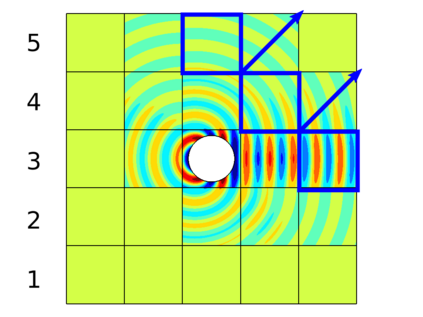
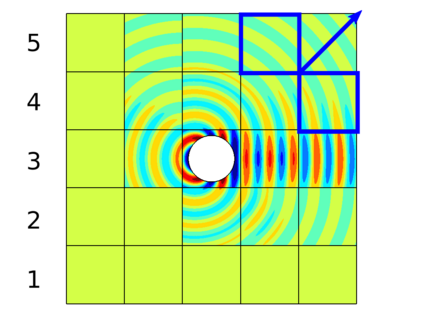
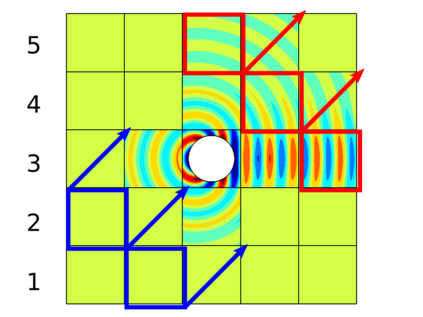
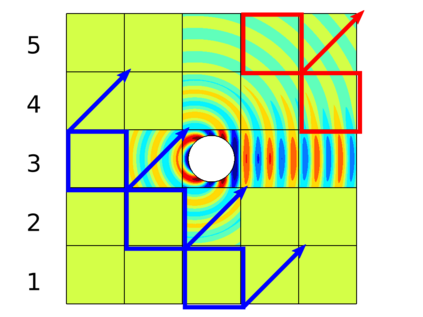
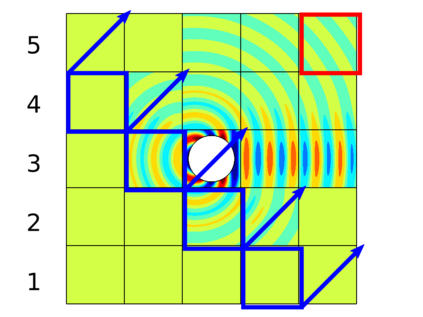
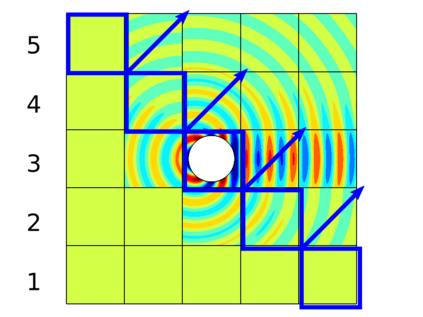
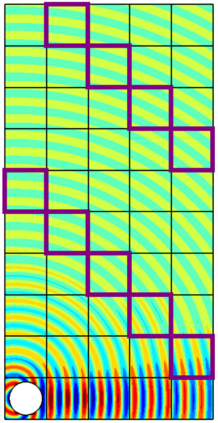
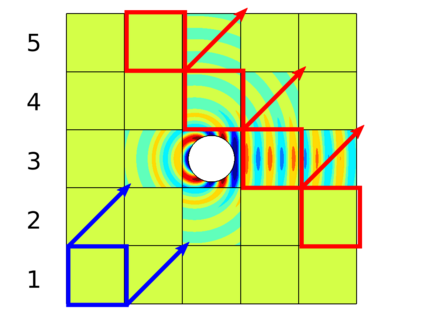
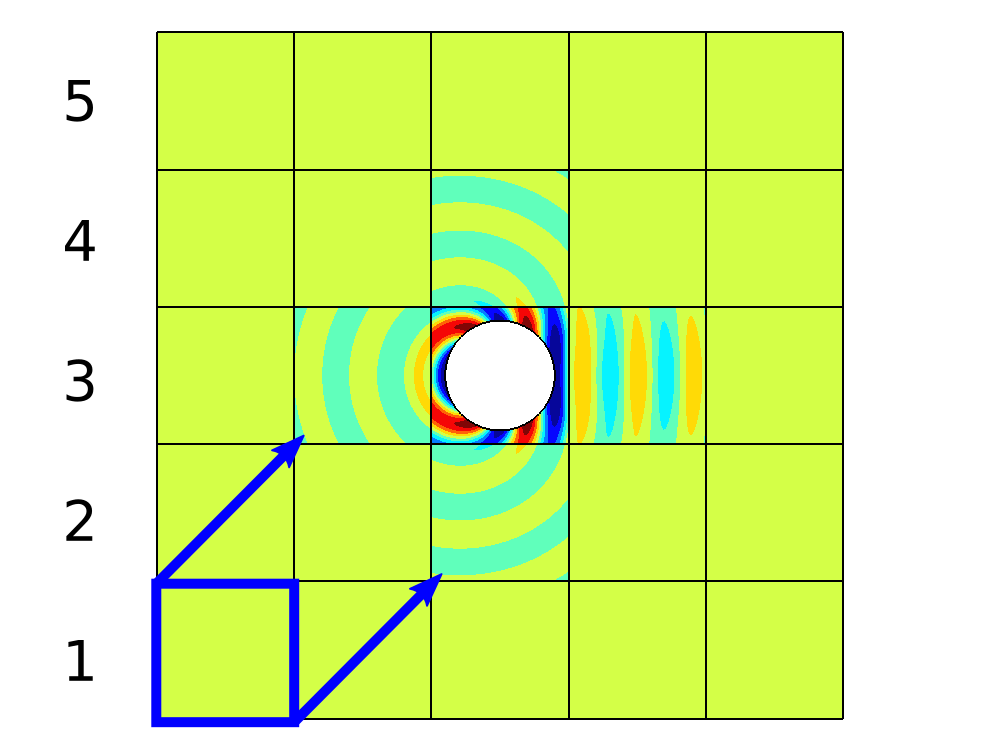
In recent research, the parallel performances of sweeping-type algorithms for high-frequency time-harmonic wave problems have been improved by departing from standard layer-type domain decomposition and introducing a new sweeping strategy on a checkerboard-type domain decomposition, where sweeps can be performed more flexibly. These sweeps can be done by a certain number of steps, each of which provides the necessary information from subdomains solved at the current iteration to their next neighboring subdomains. Although, subproblems in these subdomains can be solved concurrently at each step, the sequential nature of the process of the sweeping approaches still exists, which limits their potential for parallelization. We propose a block Jacobi sweeping preconditioner, which is an improved variant of sweeping-type preconditioners. The new feature of these improved variants can be interpreted as several partial sweeps, which can be thought of as sweeps that operate on a subset of the subdomains in parallel. We present several two-dimensional finite element results to study and compare the sweeping preconditioner and the block Jacobi sweeping preconditioner.
翻译:近期的研究表明,高频时间谐波波问题的扫描型算法的并行性能已经通过离开标准分层域分解和引入一个新的棋盘型域分解策略来提高,其中扫描可以更灵活地进行。这些扫描可以通过一定数量的步骤来完成,每个步骤都提供了来自当前迭代中解决的子域的必要信息到它们的下一个相邻的子域。尽管这些子域中的子问题可以在每个步骤中同时求解,但扫描方法的顺序性质仍然存在,这限制了它们并行化的潜力。我们提出了一种分块雅可比扫描预处理器,它是扫描型预处理器的一种改进变体。这些改进变体的新特性可以被解释为几个局部扫描,可以被认为是在子域的子集上同时进行的扫描。我们提供了几个二维有限元结果来研究和比较扫描预处理器和分块雅可比扫描预处理器。