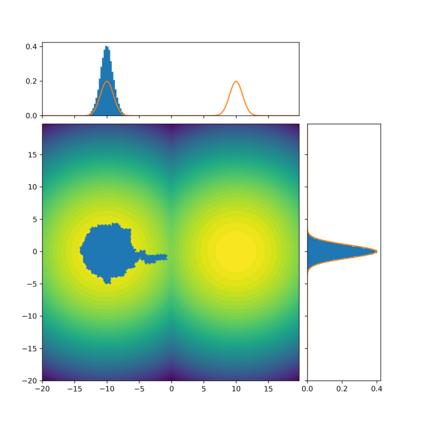
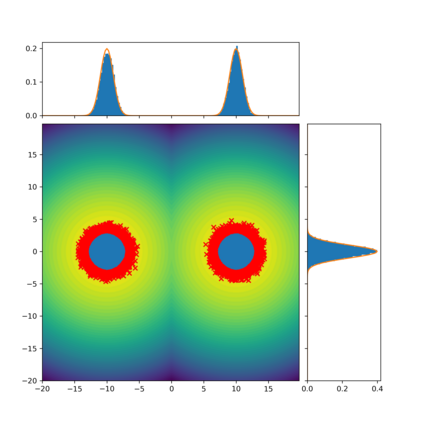
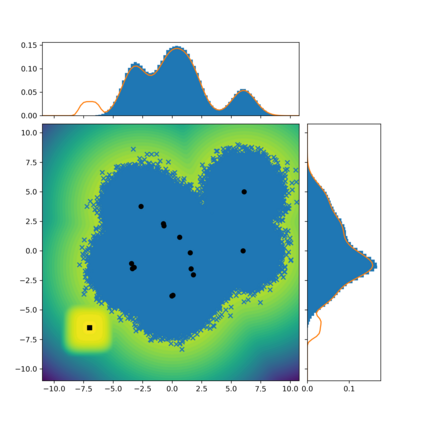
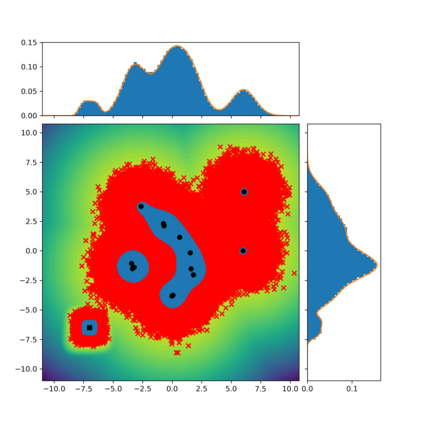
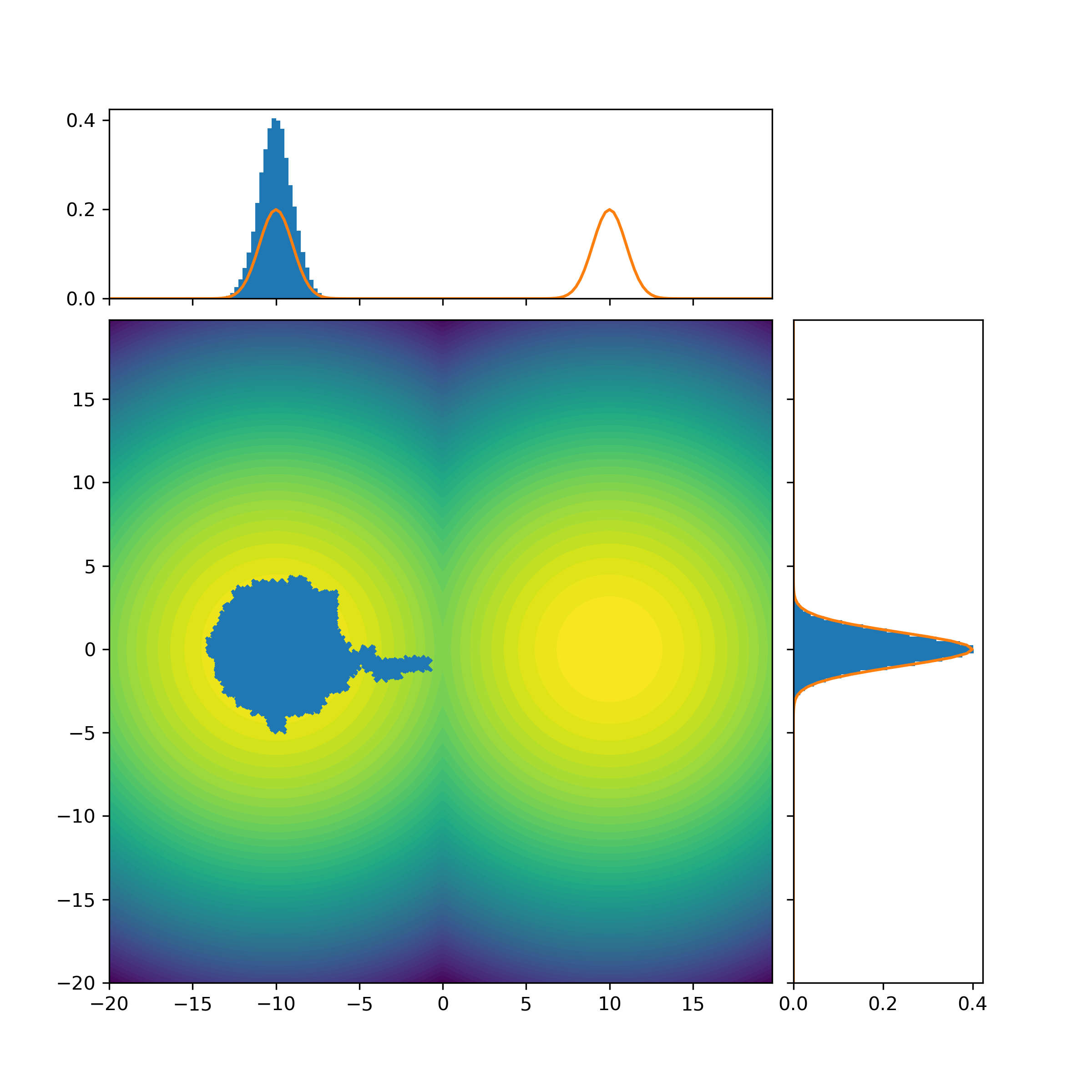
The present paper focuses on the problem of sampling from a given target distribution $\pi$ defined on some general state space. To this end, we introduce a novel class of non-reversible Markov chains, each chain being defined on an extended state space and having an invariant probability measure admitting $\pi$ as a marginal distribution. The proposed methodology is inspired by a new formulation of Kac's theorem and allows global and local dynamics to be smoothly combined. Under mild conditions, the corresponding Markov transition kernel can be shown to be irreducible and Harris recurrent. In addition, we establish that geometric ergodicity holds under appropriate conditions on the global and local dynamics. Finally, we illustrate numerically the use of the proposed method and its potential benefits in comparison to existing Markov chain Monte Carlo (MCMC) algorithms.
翻译:本文件侧重于从某个特定目标分布点上抽样的问题。为此,我们引入了新型的非可逆马可夫链条,每个链条在扩展的州空间上都有定义,并有一个无变概率的衡量标准,允许以美元作为边际分布。提议的方法受Kac理论的新提法的启发,使全球和地方动态能够顺利地结合起来。在温和的条件下,相应的Markov过渡核心可以证明是不可减损的,Harris是经常性的。此外,我们确定,几何高度在适当的条件下保持着全球和地方动态。最后,我们用数字来说明拟议方法的使用情况及其与现有的Markov链Monte Carlo(MC)算法相比的潜在好处。