Parallel Batch-Dynamic Minimum Spanning Forest and the Efficiency of Dynamic Agglomerative Graph Clustering

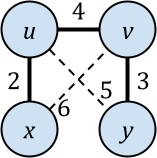
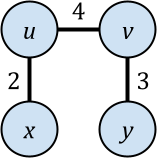
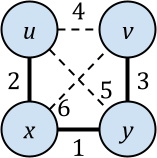
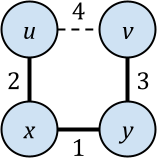
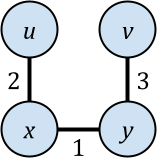
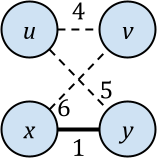
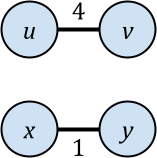
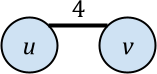
Hierarchical agglomerative clustering (HAC) is a popular algorithm for clustering data, but despite its importance, no dynamic algorithms for HAC with good theoretical guarantees exist. In this paper, we study dynamic HAC on edge-weighted graphs. As single-linkage HAC reduces to computing a minimum spanning forest (MSF), our first result is to develop a parallel batch-dynamic algorithm for maintaining MSFs. On a batch of $k$ edge insertions or deletions, our batch-dynamic MSF algorithm runs in $O(k\log^6 n)$ expected amortized work and $O(\log^4 n)$ span with high probability. It is the first fully dynamic MSF algorithm handling batches of edge updates with polylogarithmic work per update and polylogarithmic span. Using MSF, we obtain a parallel batch-dynamic algorithm that can answer queries about single-linkage graph HAC clusters. Our second result is that dynamic graph HAC is significantly harder for other common linkage functions. Assuming the strong exponential time hypothesis, dynamic graph HAC requires $\Omega(n^{1-o(1)})$ work per update or query on a graph with $n$ vertices for complete linkage, weighted average linkage, and average linkage. For complete linkage and weighted average linkage, this bound still holds even for incremental or decremental algorithms and even if we allow $\operatorname{poly}(n)$-approximation. For average linkage, the bound weakens to $\Omega(n^{1/2 - o(1)})$ for incremental and decremental algorithms, and the bounds still hold if we allow $O(n^{o(1)})$-approximation.