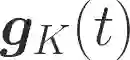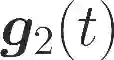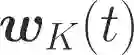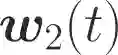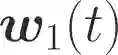One of the main focuses in distributed learning is communication efficiency, since model aggregation at each round of training can consist of millions to billions of parameters. Several model compression methods, such as gradient quantization and sparsification, have been proposed to improve the communication efficiency of model aggregation. However, the information-theoretic minimum communication cost for a given distortion of gradient estimators is still unknown. In this paper, we study the fundamental limit of communication cost of model aggregation in distributed learning from a rate-distortion perspective. By formulating the model aggregation as a vector Gaussian CEO problem, we derive the rate region bound and sum-rate-distortion function for the model aggregation problem, which reveals the minimum communication rate at a particular gradient distortion upper bound. We also analyze the communication cost at each iteration and total communication cost based on the sum-rate-distortion function with the gradient statistics of real-world datasets. It is found that the communication gain by exploiting the correlation between worker nodes is significant for SignSGD, and a high distortion of gradient estimator can achieve low total communication cost in gradient compression.
翻译:分布式学习的主要重点之一是传播效率,因为每轮培训的模型汇总可以包含数百万至数十亿个参数。一些模型压缩方法,例如梯度量化和环状化,已经提出提高模型汇总的通信效率。然而,对于梯度估计值的某种扭曲,信息理论最低通信成本仍然未知。在本文中,我们从率扭曲的角度研究模型汇总在分布式学习中的基本通信成本限制。通过将模型汇总作为矢量高斯首席执行官的问题,我们得出模型汇总问题的利率区域约束和总比率扭曲功能,这揭示了在特定的梯度扭曲上层时的最低通信率。我们还根据真实世界数据集的梯度统计,分析了每次循环的通信成本和总通信成本。我们发现,利用工人节点之间的关联产生的通信收益对于SignSGD意义重大,高度测深器的高度扭曲可以降低梯度压缩的通信成本总额。