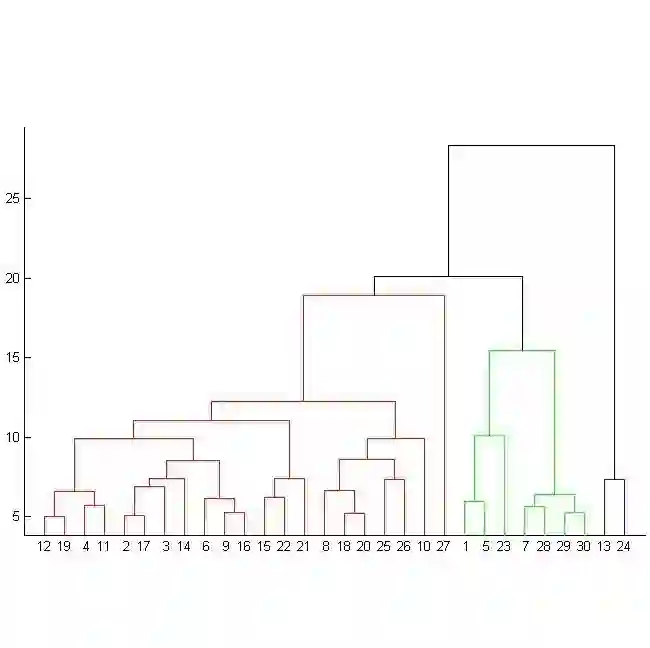
In this article we describe a new Hermite series based sequential estimator for the Spearman rank correlation coefficient and provide algorithms applicable in both the stationary and non-stationary settings. To treat the non-stationary setting, we introduce a novel, exponentially weighted estimator for the Spearman rank correlation, which allows the local nonparametric correlation of a bivariate data stream to be tracked. To the best of our knowledge this is the first algorithm to be proposed for estimating a time varying Spearman rank correlation that does not rely on a moving window approach. We explore the practical effectiveness of the Hermite series based estimators through real data and simulation studies demonstrating good practical performance. The simulation studies in particular reveal competitive performance compared to an existing algorithm. The potential applications of this work are manifold. The Hermite series based Spearman rank correlation estimator can be applied to fast and robust online calculation of correlation which may vary over time. Possible machine learning applications include, amongst others, fast feature selection and hierarchical clustering on massive data sets.
翻译:在此篇文章中, 我们描述一个新的赫尔米特序列, 以Spearman 级相关系数的顺序测算器为基础, 并提供适用于固定和非静止环境的算法。 为了处理非静止环境, 我们为Spearman 级相关比率引入了一个新颖的、 指数加权测算器, 允许跟踪双变量数据流的本地非参数性相关性。 据我们所知, 这是第一个用于估算不依赖移动窗口方法的不同时期Spearman 级相关性的算法。 我们通过真实的数据和模拟研究探索基于Hermite 级的测算器的实际有效性, 以显示良好的实用性能。 模拟研究特别揭示了与现有算法相比的竞争性性能。 这项工作的潜在应用是多重的。 基于 Spearman 级相关测量器的Hermite 系列可用于快速和稳健的在线相关关系计算, 随着时间的推移可能不同。 机器学习应用的方法包括快速特征选择和大规模数据集的分级组合等。