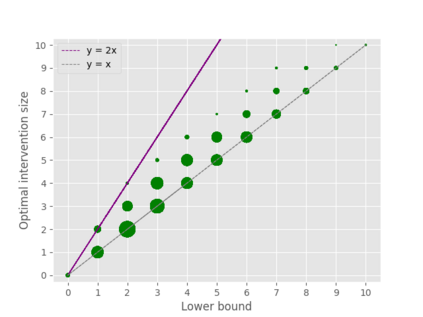
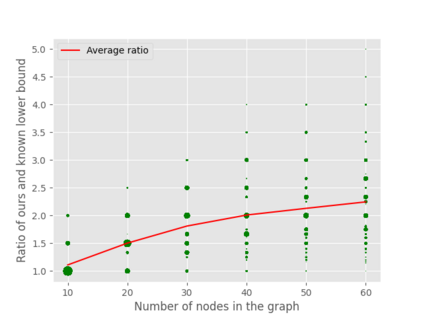
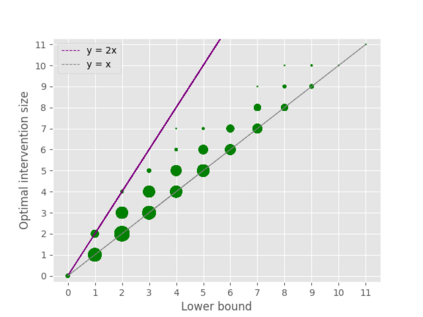
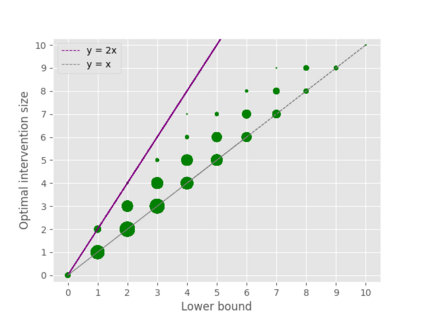
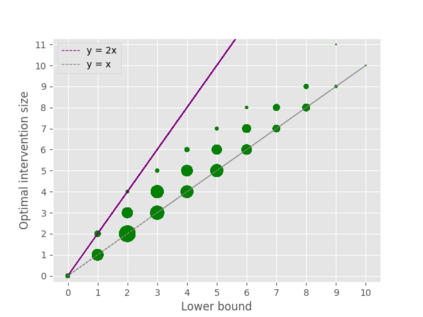
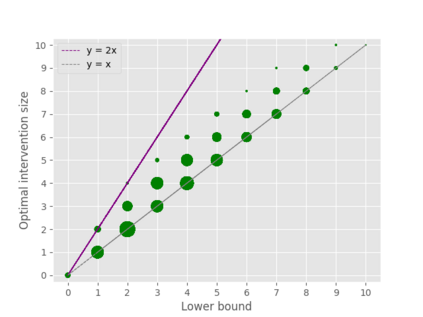
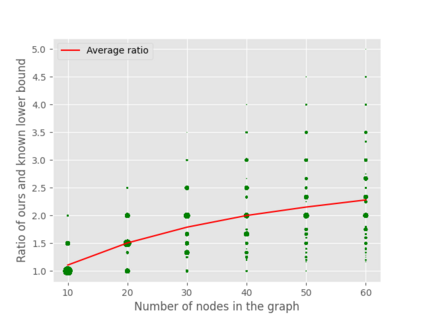
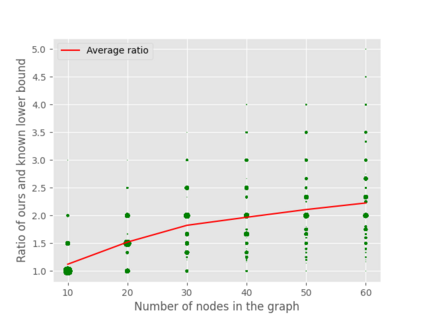
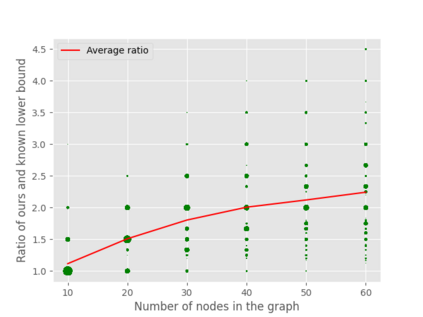
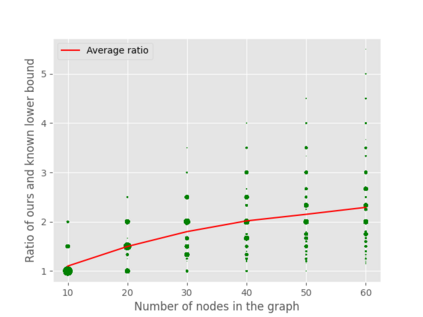
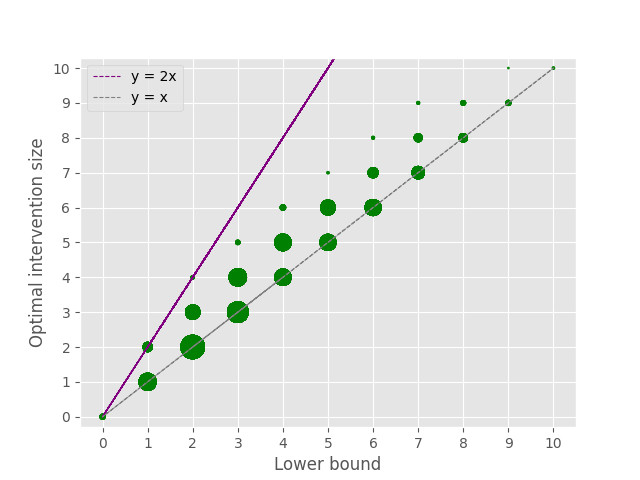
A well-studied challenge that arises in the structure learning problem of causal directed acyclic graphs (DAG) is that using observational data, one can only learn the graph up to a "Markov equivalence class" (MEC). The remaining undirected edges have to be oriented using interventions, which can be very expensive to perform in applications. Thus, the problem of minimizing the number of interventions needed to fully orient the MEC has received a lot of recent attention, and is also the focus of this work. Our first result is a new universal lower bound on the number of single-node interventions that any algorithm (whether active or passive) would need to perform in order to orient a given MEC. Our second result shows that this bound is, in fact, within a factor of two of the size of the smallest set of single-node interventions that can orient the MEC. Our lower bound is provably better than previously known lower bounds. Further, using simulations on synthetic graphs and by giving examples of special graph families, we show that our bound is often significantly better. To prove our lower bound, we develop the notion of clique-block shared-parents (CBSP) orderings, which are topological orderings of DAGs without v-structures and satisfy certain special properties. We also use the techniques developed here to extend our results to the setting of multi-node interventions.
翻译:在因果定向循环图的结构学习问题(DAG)中,一个经过深思熟虑的挑战是,使用观测数据,人们只能将图表学习到“ Markov等效类” (MEC) 。剩下的非定向边缘必须使用干预方法,这在应用中可能非常昂贵。因此,最大限度地减少充分定向MEC所需的干预数量的问题最近受到了很多关注,也是这项工作的重点。我们的第一个结果是,对于任何算法(无论是主动还是被动)为调整某个MEC而需要进行的单节式干预数量,我们有一个新的普遍较低的约束。我们的第二个结果显示,这一约束事实上是最小的单节式干预方法规模的二倍。我们较低的界限比以前已知的较低界限要好得多。此外,在合成图表上进行模拟,并举一些特殊图表家庭的例子,我们显示我们的约束往往要好得多。为了证明我们较低约束的算法,我们发展了某种特殊的干预方法,我们又不使用某种顶层的排序,我们又不使用某种顶层结构。