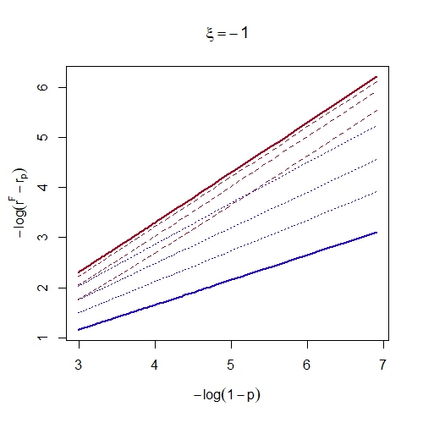
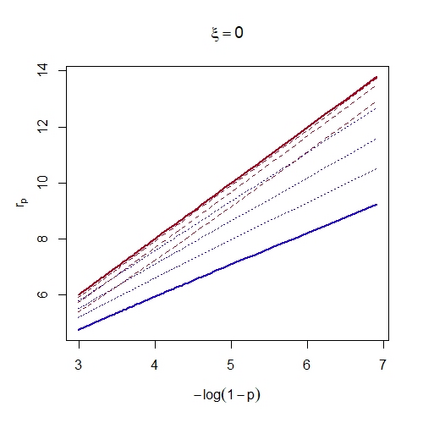
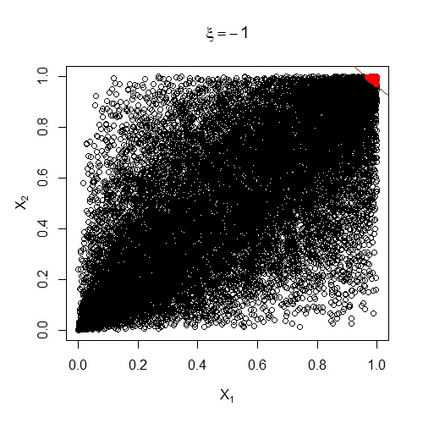
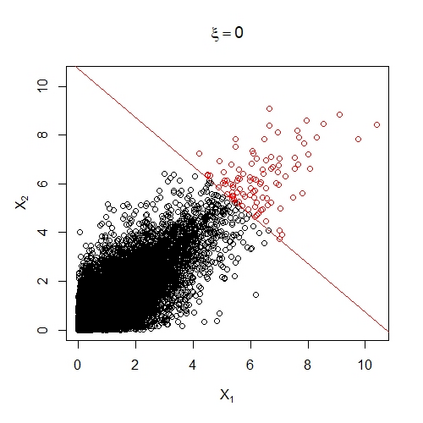
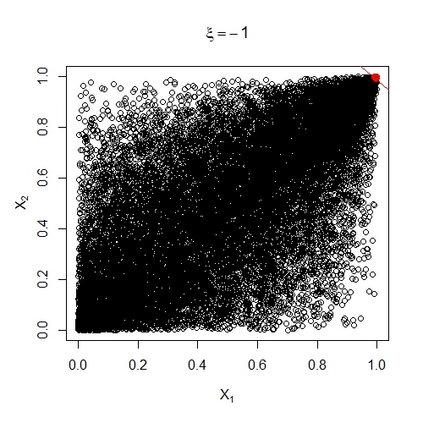
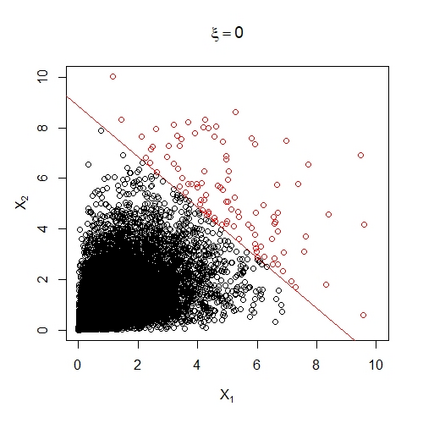
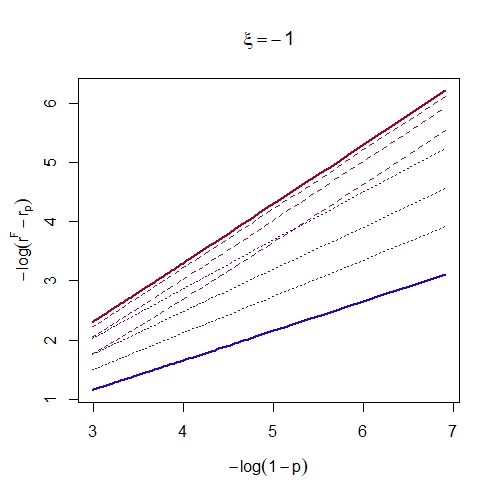
In many areas of interest, modern risk assessment requires estimation of the extremal behaviour of sums of random variables. We derive the first order upper-tail behaviour of the weighted sum of bivariate random variables under weak assumptions on their marginal distributions and their copula. The extremal behaviour of the marginal variables is characterised by the generalised Pareto distribution and their extremal dependence through subclasses of the limiting representations of Ledford and Tawn (1997) and Heffernan and Tawn (2004). We find that the upper tail behaviour of the aggregate is driven by different factors dependent on the signs of the marginal shape parameters; if they are both negative, the extremal behaviour of the aggregate is determined by both marginal shape parameters and the coefficient of asymptotic independence (Ledford and Tawn, 1996); if they are both positive or have different signs, the upper-tail behaviour of the aggregate is given solely by the largest marginal shape. We also derive the aggregate upper-tail behaviour for some well known copulae which reveals further insight into the tail structure when the copula falls outside the conditions for the subclasses of the limiting dependence representations.
翻译:在许多感兴趣的领域,现代风险评估要求估计随机变量总和的极端行为。我们得出两变随机变量加权总和的第一顺序高尾行为,假设其边际分布和阴极;边际变量的极端行为特征是泛泛的Pareto分布及其通过Ledford和Tawn(1997年)、Heffernan和Tawn(2004年)有限表述的子类的极端依赖性。我们发现,总量的上尾行为是由取决于边际形状参数迹象的不同因素驱动的;如果两者都是负面的,则总量的极端行为由边际形状参数和无症状独立系数(Ledford和Tawn,1996年)决定;如果这些边际变量是正面的或有不同迹象,则总量的上尾部行为完全由最大的边际形状给出。我们还从一些广为人知的椰菜的总的上尾行为中得出,当椰菜在限制依赖性代表的子类别的条件之外时会进一步洞察尾结构。