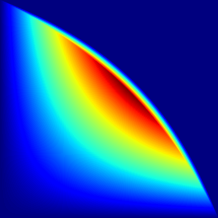
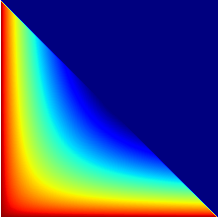
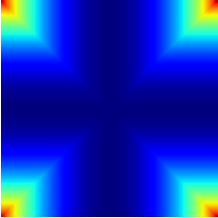
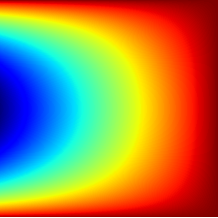
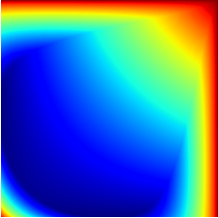
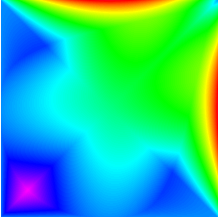
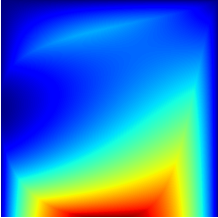
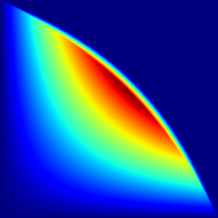
A crucial step towards the 6th generation (6G) of networks would be a shift in communication paradigm beyond the limits of Shannon's theory. In both classical and quantum Shannon's information theory, communication channels are generally assumed to combine through classical trajectories, so that the associated network path traversed by the information carrier is well-defined. Counter-intuitively, quantum mechanics enables a quantum information carrier to propagate through a quantum path, i.e., through a path such that the causal order of the constituting communications channels becomes indefinite. Quantum paths exhibit astonishing features, such as providing non-null capacity even when no information can be sent through any classical path. In this paper, we study the quantum capacity achievable via a quantum path and establish upper and the lower bounds for it. Our findings reveal the substantial advantage achievable with a quantum path over any classical placements of communications channels in terms of ultimate achievable communication rates. Furthermore, we identify the region where a quantum path incontrovertibly outperforms the amount of transmissible information beyond the limits of conventional quantum Shannon's theory, and we quantify this advantage over classical paths through a conservative estimate.
翻译:迈向第六代(6G)网络的关键一步,是改变通讯范式,超越香农(Shannon)理论的极限。无论是在古典还是量子香农的信息理论中,通讯信道一般都通过经典轨迹相结合,因此信息载体所穿越的相关网络路径也是明确定义的。令人惊讶的是,量子力学使得量子信息载体能够通过一种称为“量子路径”的方式进行传播,即通过一条路径,使得通讯信道的因果性被沿途的通讯信道组成模糊不清。量子路径具有惊人的特点,例如即使在经典路径上无法发送任何信息的情况下,它也能提供非零的通讯容量。在本文中,我们研究了通过量子路径可以实现的量子容量,并建立了其上下界。我们的研究结果显示,相较于任何经典通讯信道位置布局,通过量子路径实现的通讯速率具有巨大的优势。此外,我们还确定了量子路径在哪个区域无可争议地超越常规量子香农理论下可传输信息的数量,并通过保守估计量化了这种优势。