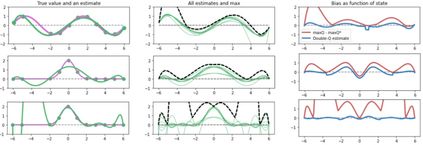
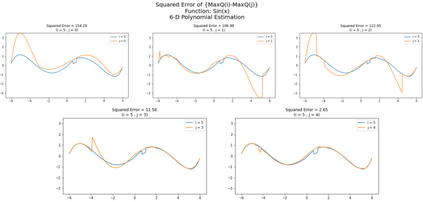
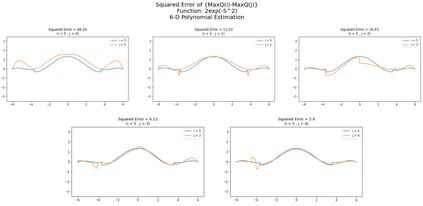
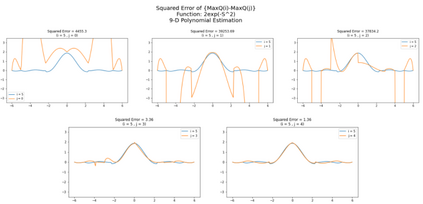
Inspired by double q learning algorithm, the double DQN algorithm was originally proposed in order to address the overestimation issue in the original DQN algorithm. The double DQN has successfully shown both theoretically and empirically the importance of decoupling in terms of action evaluation and selection in computation of targets values; although, all the benefits were acquired with only a simple adaption to DQN algorithm, minimal possible change as it was mentioned by the authors. Nevertheless, there seems a roll-back in the proposed algorithm of Double-DQN since the parameters of policy network are emerged again in the target value function which were initially withdrawn by DQN with the hope of tackling the serious issue of moving targets and the instability caused by it (i.e., by moving targets) in the process of learning. Therefore, in this paper three modifications to the Double-DQN algorithm are proposed with the hope of maintaining the performance in the terms of both stability and overestimation. These modifications are focused on the logic of decoupling the best action selection and evaluation in the target value function and the logic of tackling the moving targets issue. Each of these modifications have their own pros and cons compared to the others. The mentioned pros and cons mainly refer to the execution time required for the corresponding algorithm and the stability provided by the corresponding algorithm. Also, in terms of overestimation, none of the modifications seem to underperform compared to the original Double-DQN if not outperform it. With the intention of evaluating the efficacy of the proposed modifications, multiple empirical experiments along with theoretical experiments were conducted. The results obtained are represented and discussed in this article.
翻译:在双q学习算法的启发下,最初提出了双重的DQN算法,以解决原DQN算法中过高估计的问题。双DQN算法在理论上和经验上都成功地表明,在计算目标值时,在行动评价和选择方面,在行动评价和选择方面,必须脱钩;尽管所有好处都是在简单适应DQN算法的情况下获得的,但正如作者所提到的那样,可能作出的改变是最小的。然而,拟议的双DQN算法似乎出现了倒退,因为政策网络参数再次出现在目标值函数中,而目标值函数最初被DQN撤回,希望解决移动目标的严重问题和由此造成的不稳定性(即通过移动目标)在学习过程中。因此,本文建议对双QN算法作三次修改,希望既保持稳定性,也保持过高的估计。这些修改的逻辑是分解目标值函数中最佳行动选择和评价的逻辑,以及处理移动目标的逻辑最初值函数的最初值函数,希望解决移动目标的严重问题(即通过移动目标)在学习过程中(即通过移动目标)中(即移动目标)的不稳定性评估效率问题(即通过移动目标目标),因此,每项是提出对双Q算法的修改,这些修正的逻辑,这些逻辑,这些修正看来是相对的逻辑,在进行。这些修正,这些修正的逻辑,这些修正是相对于的逻辑,这些修正是比较的逻辑,这些逻辑,这些逻辑,这些修正是相对的变法的变的变的变的变的变。