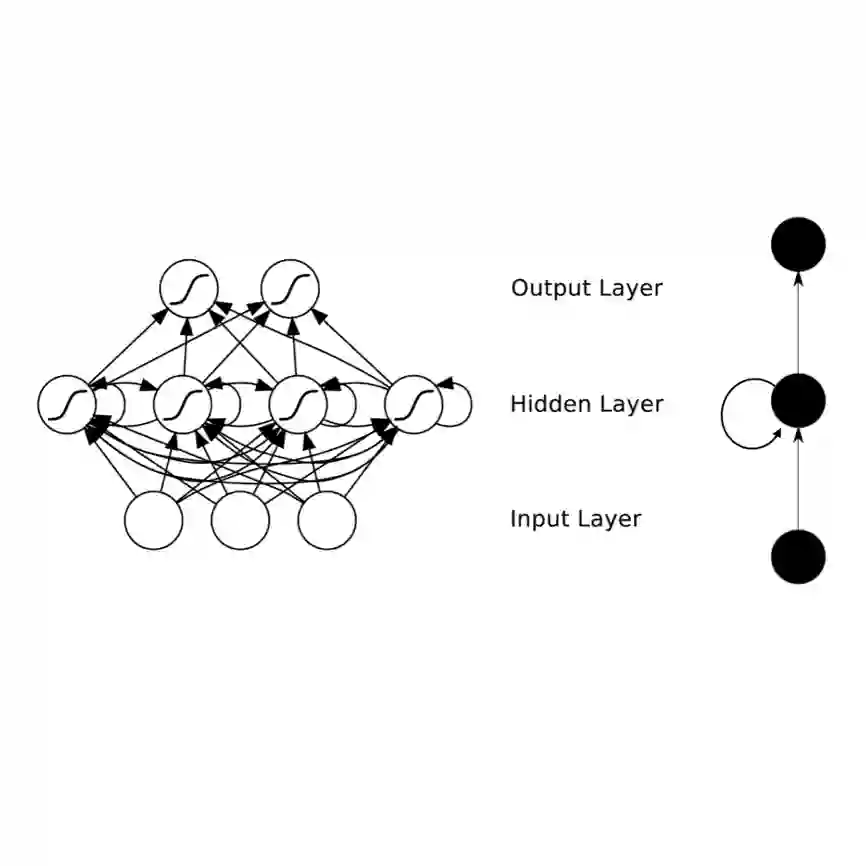
Viewing recurrent neural networks (RNNs) as continuous-time dynamical systems, we propose a recurrent unit that describes the hidden state's evolution with two parts: a well-understood linear component plus a Lipschitz nonlinearity. This particular functional form facilitates stability analysis of the long-term behavior of the recurrent unit using tools from nonlinear systems theory. In turn, this enables architectural design decisions before experimentation. Sufficient conditions for global stability of the recurrent unit are obtained, motivating a novel scheme for constructing hidden-to-hidden matrices. Our experiments demonstrate that the Lipschitz RNN can outperform existing recurrent units on a range of benchmark tasks, including computer vision, language modeling and speech prediction tasks. Finally, through Hessian-based analysis we demonstrate that our Lipschitz recurrent unit is more robust with respect to input and parameter perturbations as compared to other continuous-time RNNs.
翻译:将经常性神经网络(RNN)视为连续时动态系统,我们提出一个经常性单元,用两部分来描述隐藏状态的演变:一个深为理解的线性组件,加上一个不直线性部分。这种特定的功能形式有助于利用非线性系统理论的工具对经常性单位的长期行为进行稳定分析。反过来,这又使得在实验之前就能够作出建筑设计决定。为经常性单位的全球稳定创造足够的条件,鼓励建立一个建造隐藏至隐藏矩阵的新计划。我们的实验表明,利普西茨网络可以在一系列基准任务上比现有的经常性单位更完善,包括计算机视觉、语言模型和语言预测任务。最后,通过基于赫斯安的分析,我们证明我们的利普西茨经常性单位与其他连续时间的RNNP相比,在输入和参数穿透方面更加强大。