Neural Networks asymptotic behaviours suitable for the resolution of inverse problems

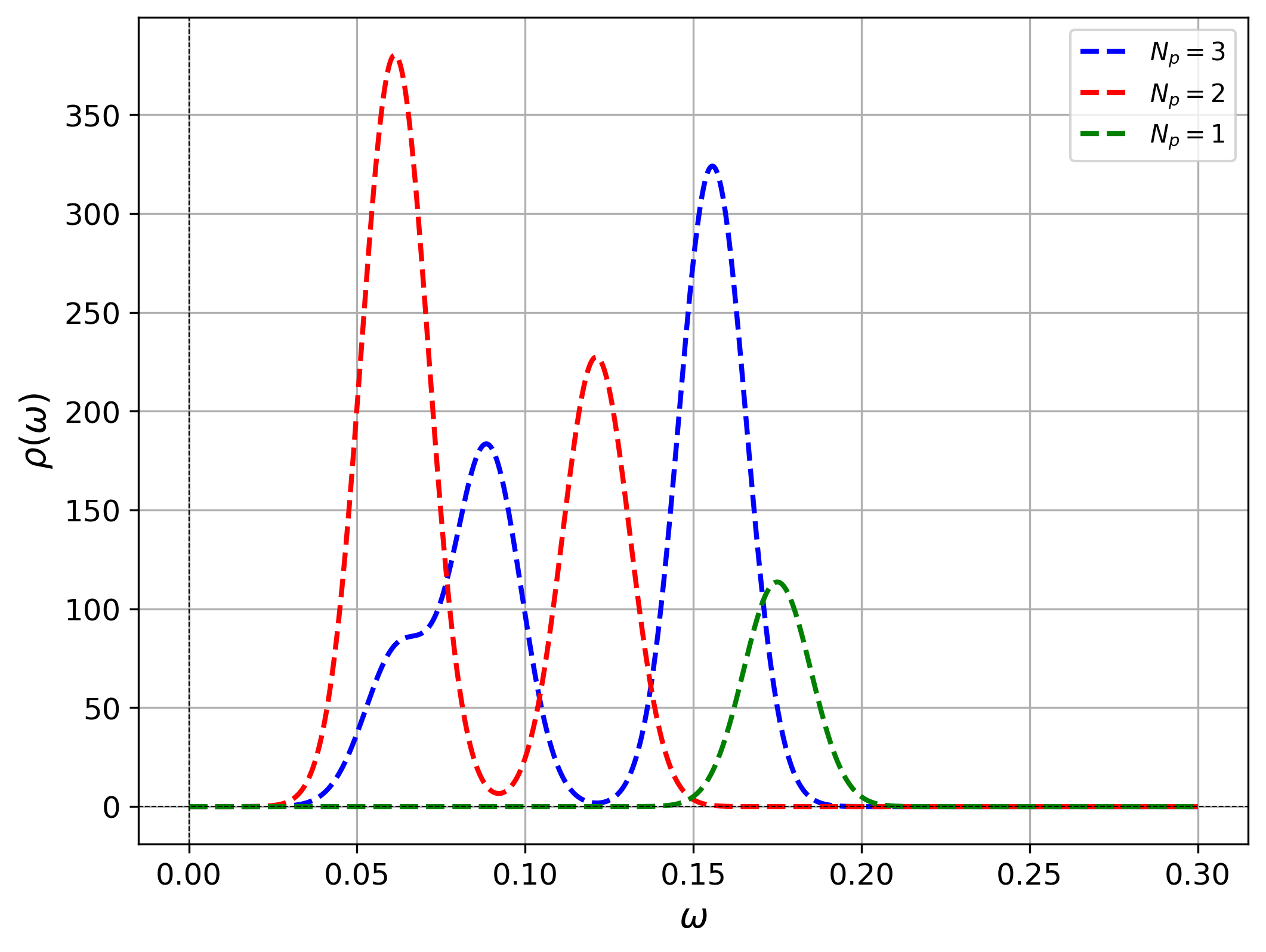
In this paper, we perform a study on the effectiveness of Neural Network (NN) techniques for deconvolution inverse problems. We consider NN's asymptotic limits, corresponding to Gaussian Processes (GPs), where parameter non-linearities are lost. Using these resulting GPs, we address the deconvolution inverse problem in the case of a quantum harmonic oscillator simulated through Monte Carlo techniques on a lattice. A scenario with a known analytical solution. Our findings indicate that solving the deconvolution inverse problem with a fully connected NN yields less performing results than those obtained using the GPs derived from NN's asymptotic limits. Furthermore, we observe the trained NN's accuracy approaching that of GPs with increasing layer width. Notably, one of these GPs defies interpretation as a probabilistic model, offering a novel perspective compared to established methods in the literature. Additionally, the NNs, in their asymptotic limit, provide cost-effective analytical solutions.