Deep Calibration of Interest Rates Model

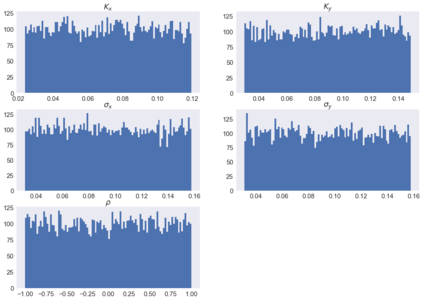
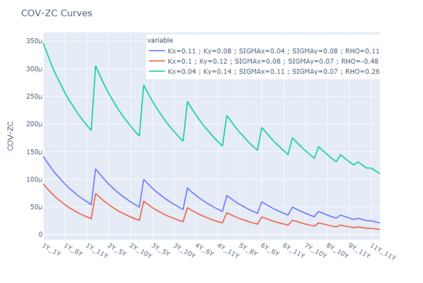
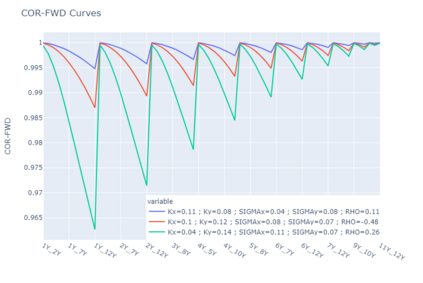
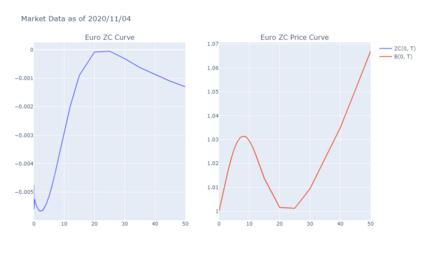
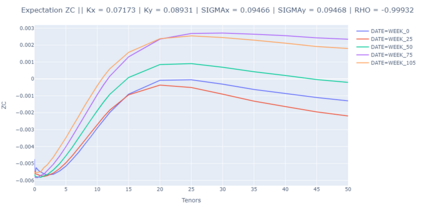
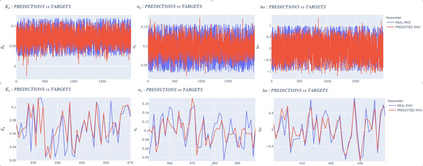
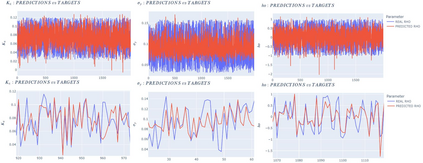
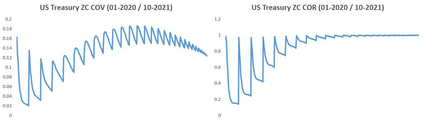
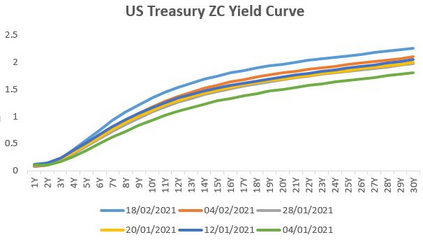
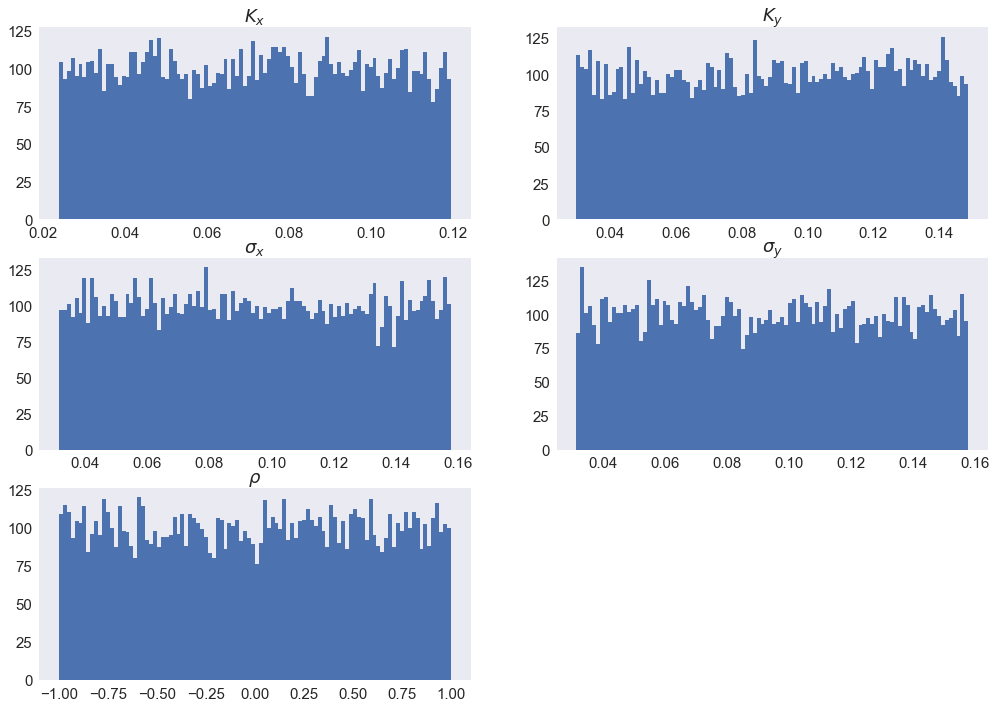
For any financial institution it is a necessity to be able to apprehend the behavior of interest rates. Despite the use of Deep Learning that is growing very fastly, due to many reasons (expertise, ease of use, ...) classic rates models such as CIR, or the Gaussian family are still being used widely. We propose to calibrate the five parameters of the G2++ model using Neural Networks. To achieve that, we construct synthetic data sets of parameters drawn uniformly from a reference set of parameters calibrated from the market. From those parameters, we compute Zero-Coupon and Forward rates and their covariances and correlations. Our first model is a Fully Connected Neural network and uses only covariances and correlations. We show that covariances are more suited to the problem than correlations. The second model is a Convulutional Neural Network using only Zero-Coupon rates with no transformation. The methods we propose perform very quickly (less than 0.3 seconds for 2 000 calibrations) and have low errors and good fitting.