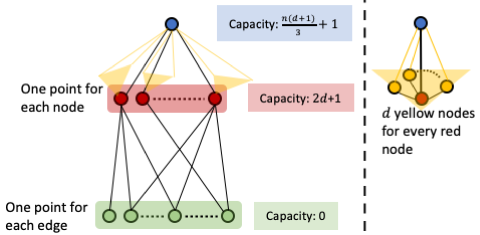
We consider the capacitated clustering problem in general metric spaces where the goal is to identify $k$ clusters and minimize the sum of the radii of the clusters (we call this the Capacitated-$k$-sumRadii problem). We are interested in fixed-parameter tractable (FPT) approximation algorithms where the running time is of the form $f(k) \cdot \text{poly}(n)$, where $f(k)$ can be an exponential function of $k$ and $n$ is the number of points in the input. In the uniform capacity case, Bandyapadhyay et al. recently gave a $4$-approximation algorithm for this problem. Our first result improves this to an FPT $3$-approximation and extends to a constant factor approximation for any $L_p$ norm of the cluster radii. In the general capacities version, Bandyapadhyay et al. gave an FPT $15$-approximation algorithm. We extend their framework to give an FPT $(4 + \sqrt{13})$-approximation algorithm for this problem. Our framework relies on a novel idea of identifying approximations to optimal clusters by carefully pruning points from an initial candidate set of points. This is in contrast to prior results that rely on guessing suitable points and building balls of appropriate radii around them. On the hardness front, we show that assuming the Exponential Time Hypothesis, there is a constant $c > 1$ such that any $c$-approximation algorithm for the non-uniform capacity version of this problem requires running time $2^{\Omega \left(\frac{k}{polylog(k)} \right)}$.
翻译:暂无翻译