On the Convergence and Sample Efficiency of Variance-Reduced Policy Gradient Method

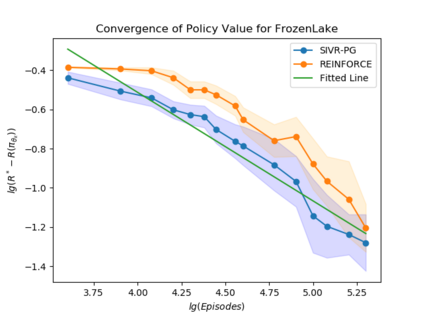
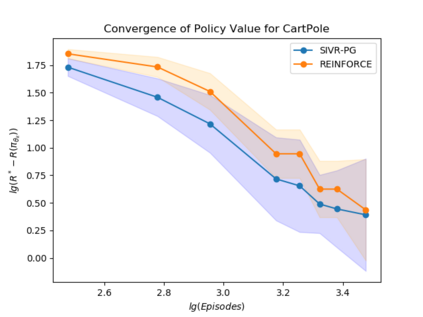
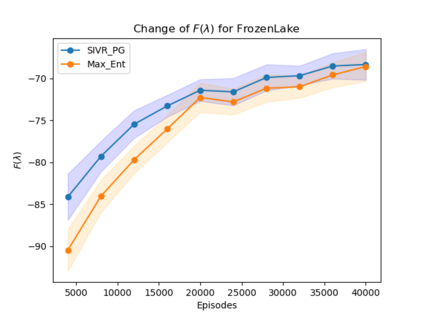
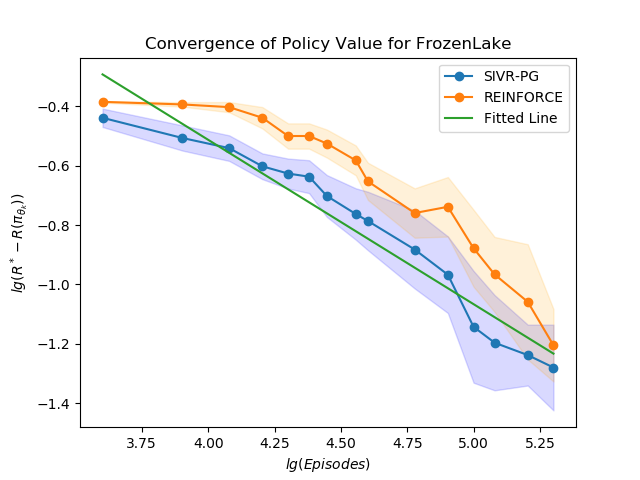
Policy gradient gives rise to a rich class of reinforcement learning (RL) methods, for example the REINFORCE. Yet the best known sample complexity result for such methods to find an $\epsilon$-optimal policy is $\mathcal{O}(\epsilon^{-3})$, which is suboptimal. In this paper, we study the fundamental convergence properties and sample efficiency of first-order policy optimization method. We focus on a generalized variant of policy gradient method, which is able to maximize not only a cumulative sum of rewards but also a general utility function over a policy's long-term visiting distribution. By exploiting the problem's hidden convex nature and leveraging techniques from composition optimization, we propose a Stochastic Incremental Variance-Reduced Policy Gradient (SIVR-PG) approach that improves a sequence of policies to provably converge to the global optimal solution and finds an $\epsilon$-optimal policy using $\tilde{\mathcal{O}}(\epsilon^{-2})$ samples.