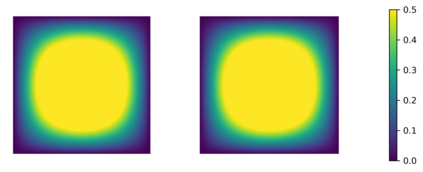
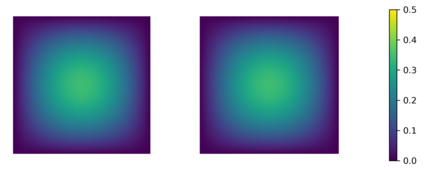
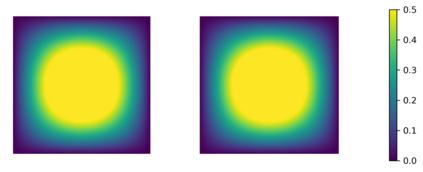
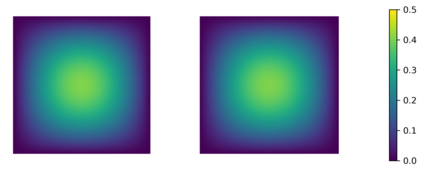
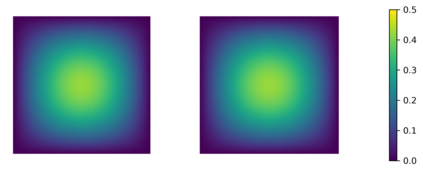
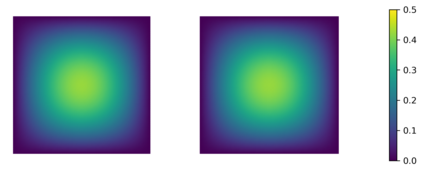
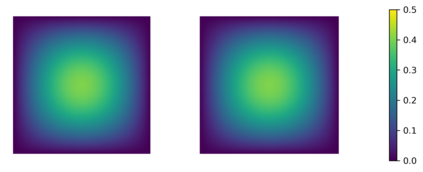
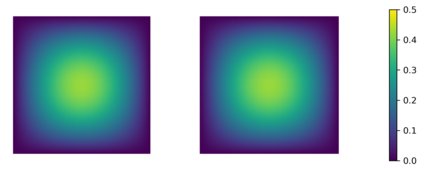
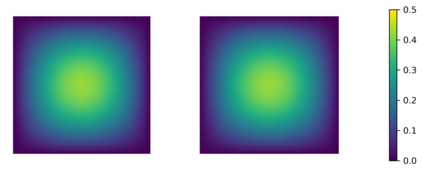
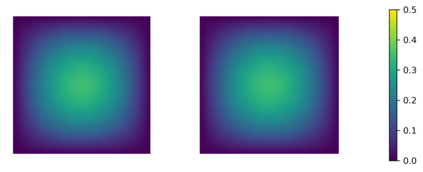
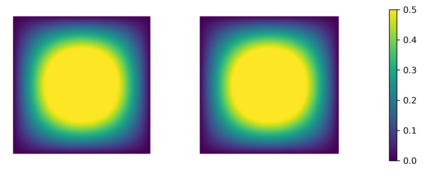
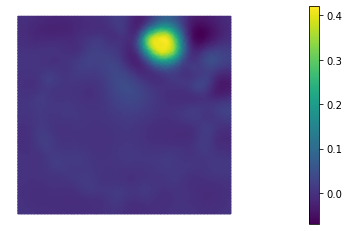
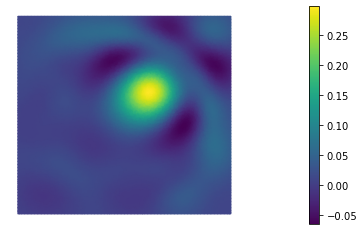
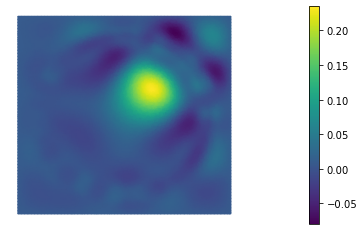
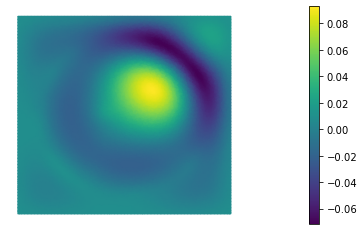
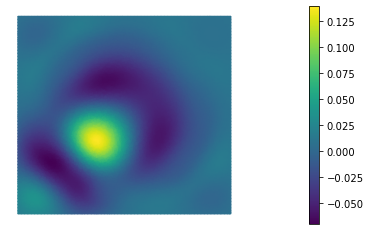
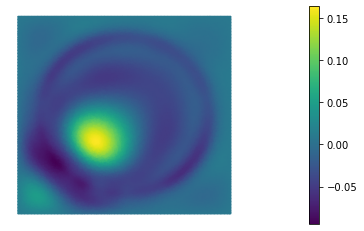
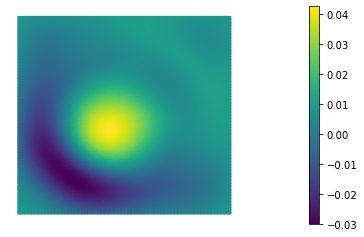
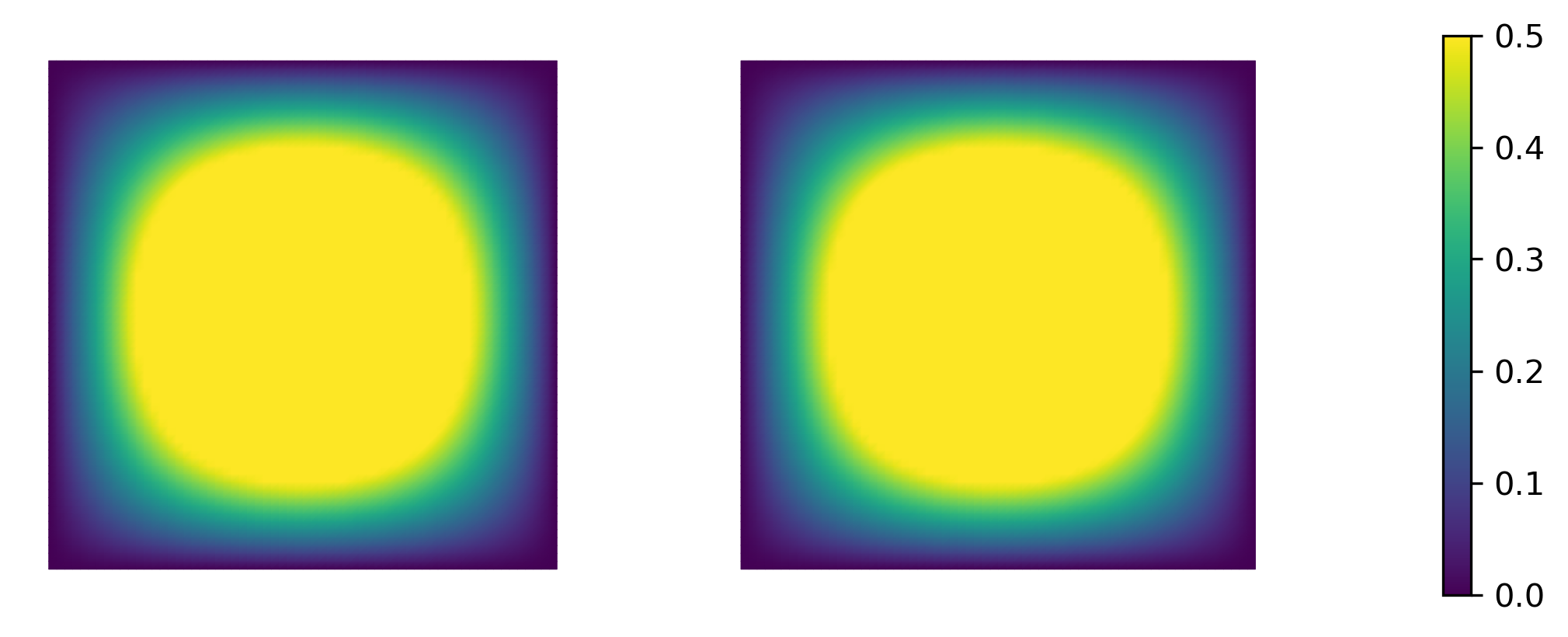
In this paper we consider the inverse problem of identifying the initial data in a fractionally damped wave equation from time trace measurements on a surface, as relevant in photoacoustic or thermoacoustic tomography. We derive and analyze a time stepping method for the numerical solution of the corresponding forward problem. Moreover, to efficiently obtain reconstructions by minimizing a Tikhonov regularization functional (or alternatively, by computing the MAP estimator in a Bayesian approach), we develop an adjoint based scheme for gradient computation. Numerical reconstructions in two space dimensions illustrate the performance of the devised methods.
翻译:在本文中,我们考虑了从表面时间痕量测量中分片倾斜的波方程确定初始数据的逆向问题,这与光声学或热声学摄影相关。我们得出和分析了用于数字解决相应前方问题的时间步法。此外,通过尽量减少Tikhonov的正规化功能(或者通过在贝叶西亚方法中计算MAP估测器)来有效实现重建,我们开发了一个基于梯度计算的联合计划。两个空间层面的数值重建显示了设计方法的性能。