Towards a Theoretical Framework of Out-of-Distribution Generalization

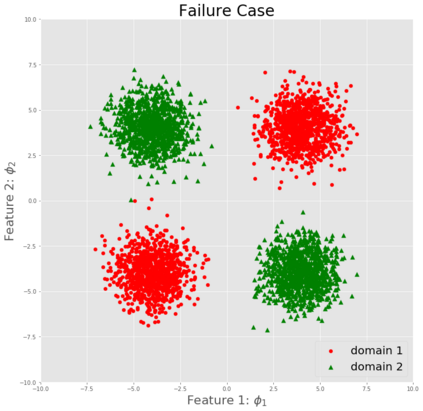
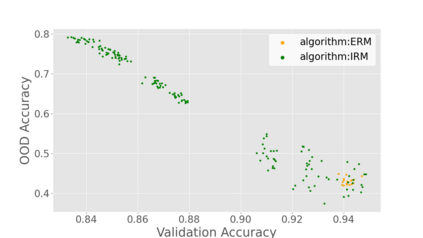
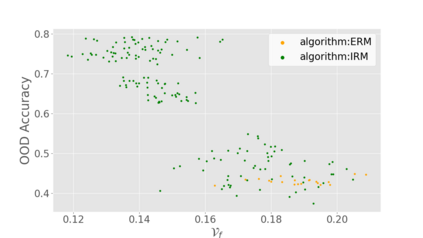
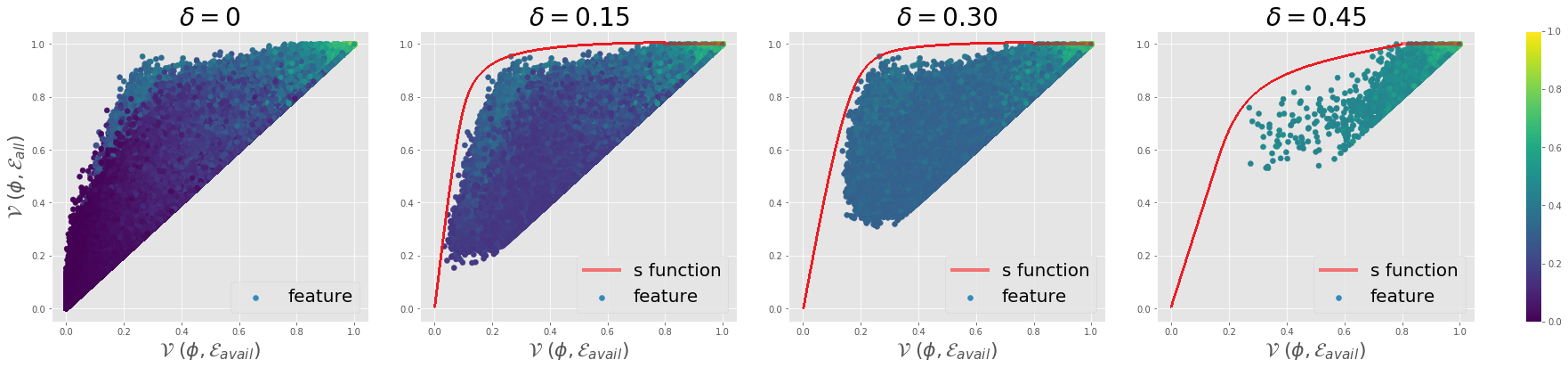
Generalization to out-of-distribution (OOD) data, or domain generalization, is one of the central problems in modern machine learning. Recently, there is a surge of attempts to propose algorithms for OOD that mainly build upon the idea of extracting invariant features. Although intuitively reasonable, theoretical understanding of what kind of invariance can guarantee OOD generalization is still limited, and generalization to arbitrary out-of-distribution is clearly impossible. In this work, we take the first step towards rigorous and quantitative definitions of 1) what is OOD; and 2) what does it mean by saying an OOD problem is learnable. We also introduce a new concept of expansion function, which characterizes to what extent the variance is amplified in the test domains over the training domains, and therefore give a quantitative meaning of invariant features. Based on these, we prove OOD generalization error bounds. It turns out that OOD generalization largely depends on the expansion function. As recently pointed out by Gulrajani and Lopez-Paz (2020), any OOD learning algorithm without a model selection module is incomplete. Our theory naturally induces a model selection criterion. Extensive experiments on benchmark OOD datasets demonstrate that our model selection criterion has a significant advantage over baselines.