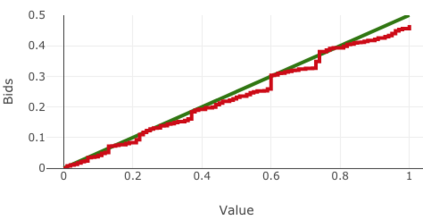
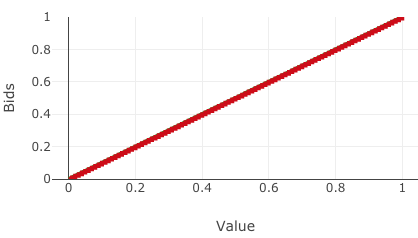
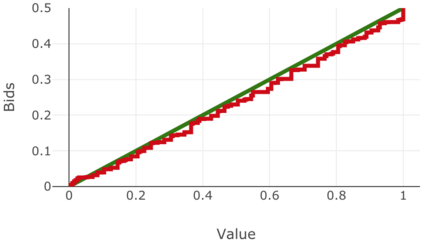
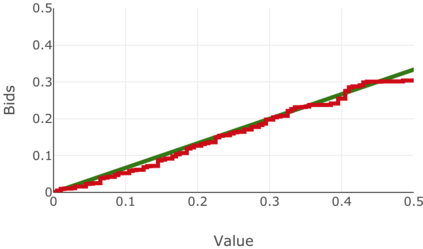
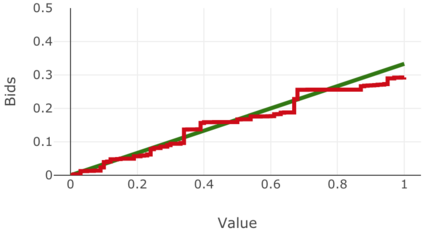
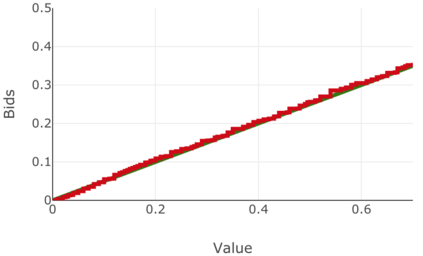
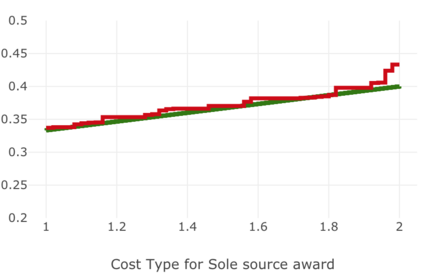
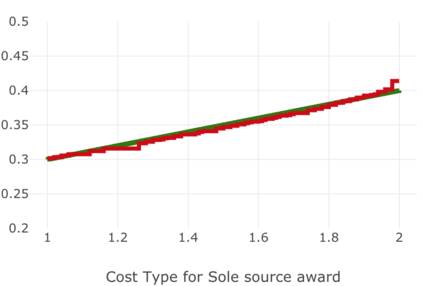
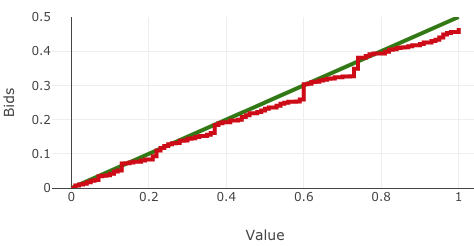
We present a best-response based algorithm for computing verifiable $\varepsilon$-perfect Bayesian equilibria for sequential auctions with combinatorial bidding spaces and incomplete information. Previous work has focused only on computing Bayes-Nash equilibria for static single-round auctions, which our work captures as a special case. Additionally, we prove an upper bound $\varepsilon$ on the utility loss of our approximate equilibria and present an algorithm to efficiently compute $\varepsilon$ based on the immediate loss at each subgame. We evaluate the performance of our algorithm by reproducing known results from several auctions previously introduced in the literature, including a model of combinatorial split-award auctions used in procurement.
翻译:暂无翻译