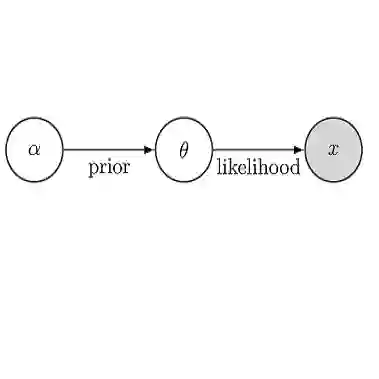
The integrated nested Laplace approximations (INLA) method has become a widely utilized tool for researchers and practitioners seeking to perform approximate Bayesian inference across various fields of application. To address the growing demand for incorporating more complex models and enhancing the method's capabilities, this paper introduces a novel framework that leverages dense matrices for performing approximate Bayesian inference based on INLA across multiple computing nodes using HPC. When dealing with non-sparse precision or covariance matrices, this new approach scales better compared to the current INLA method, capitalizing on the computational power offered by multiprocessors in shared and distributed memory architectures available in contemporary computing resources and specialized dense matrix algebra. To validate the efficacy of this approach, we conduct a simulation study then apply it to analyze cancer mortality data in Spain, employing a three-way spatio-temporal interaction model.
翻译:暂无翻译