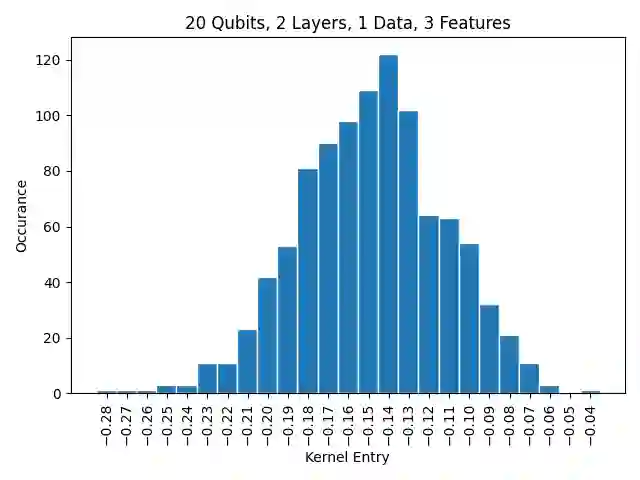
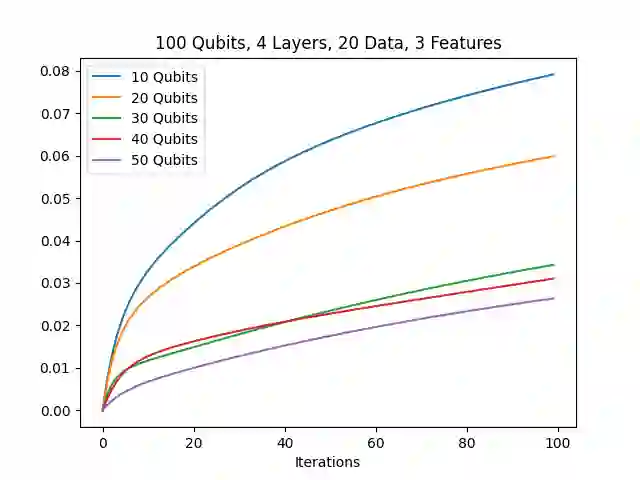
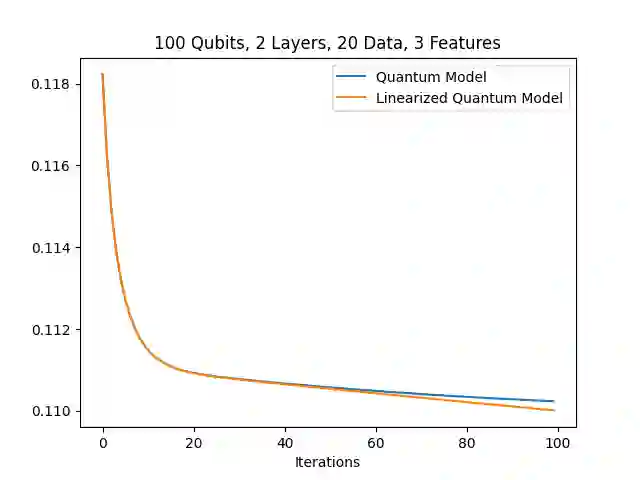
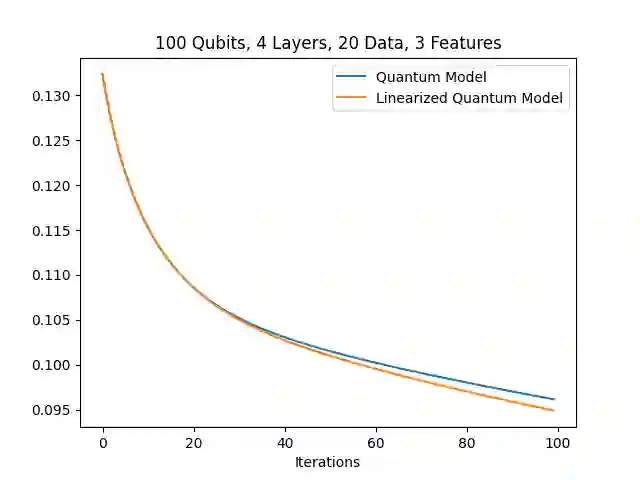
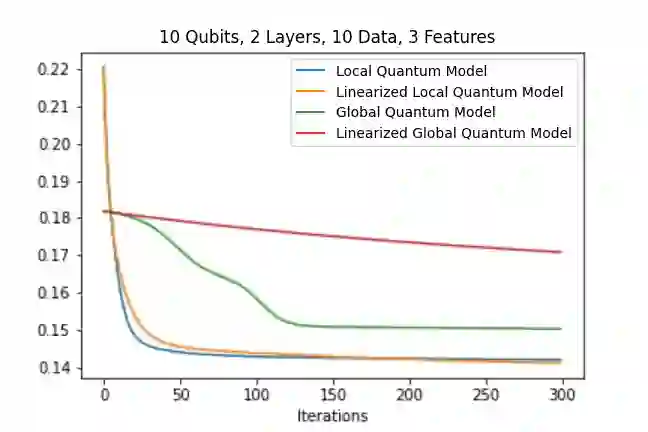
In the training of over-parameterized model functions via gradient descent, sometimes the parameters do not change significantly and remain close to their initial values. This phenomenon is called lazy training, and motivates consideration of the linear approximation of the model function around the initial parameters. In the lazy regime, this linear approximation imitates the behavior of the parameterized function whose associated kernel, called the tangent kernel, specifies the training performance of the model. Lazy training is known to occur in the case of (classical) neural networks with large widths. In this paper, we show that the training of geometrically local parameterized quantum circuits enters the lazy regime for large numbers of qubits. More precisely, we prove bounds on the rate of changes of the parameters of such a geometrically local parameterized quantum circuit in the training process, and on the precision of the linear approximation of the associated quantum model function; both of these bounds tend to zero as the number of qubits grows. We support our analytic results with numerical simulations.
翻译:在通过梯度下降来训练过度参数模型函数的过程中,参数有时不会发生重大变化,而且仍然接近最初值。这一现象被称为懒惰训练,并促使考虑模型函数围绕初始参数的线性近似。在懒惰的状态下,这种线性近近似模仿参数化函数的行为,其相关内核被称为淡色内核,它规定了模型的培训性能。已知在(古典)大宽度的神经网络中,进行懒惰训练。在本文中,我们显示对几何本地参数化量子电路的培训进入大量qubit的懒惰状态。更准确地说,我们证明,在培训过程中,这种几何式本地参数化量子电路的参数变化速度,以及相关量子模型函数的线性近近度的精确度是一定的。随着qubits数量的增长,这两条线性的培训往往为零。我们用数字模拟来支持我们的解析结果。