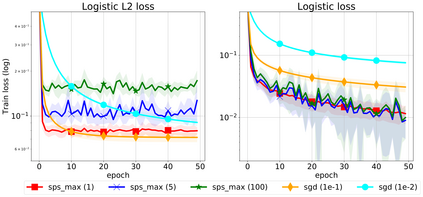
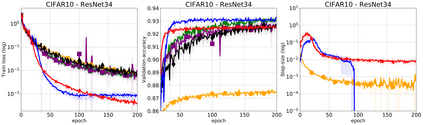
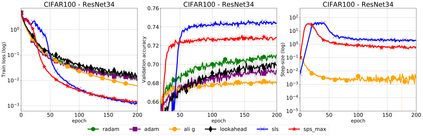
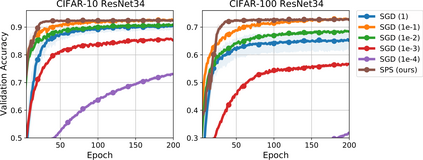
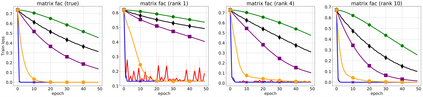
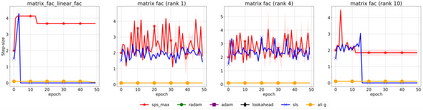
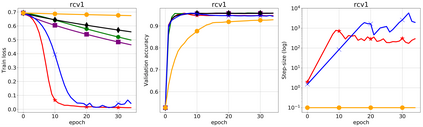
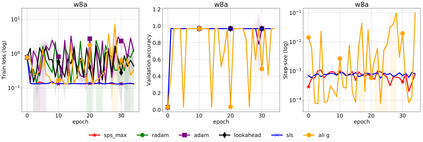
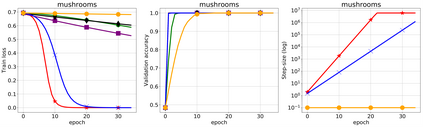
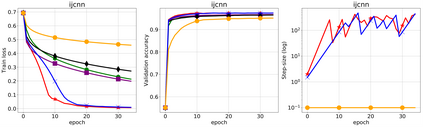
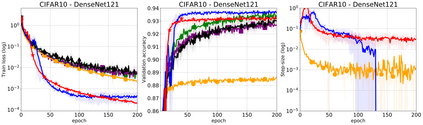
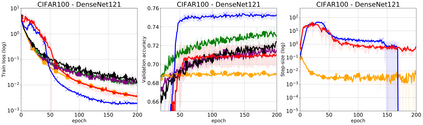
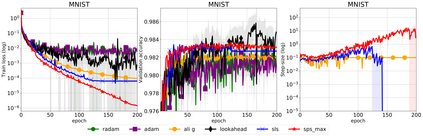
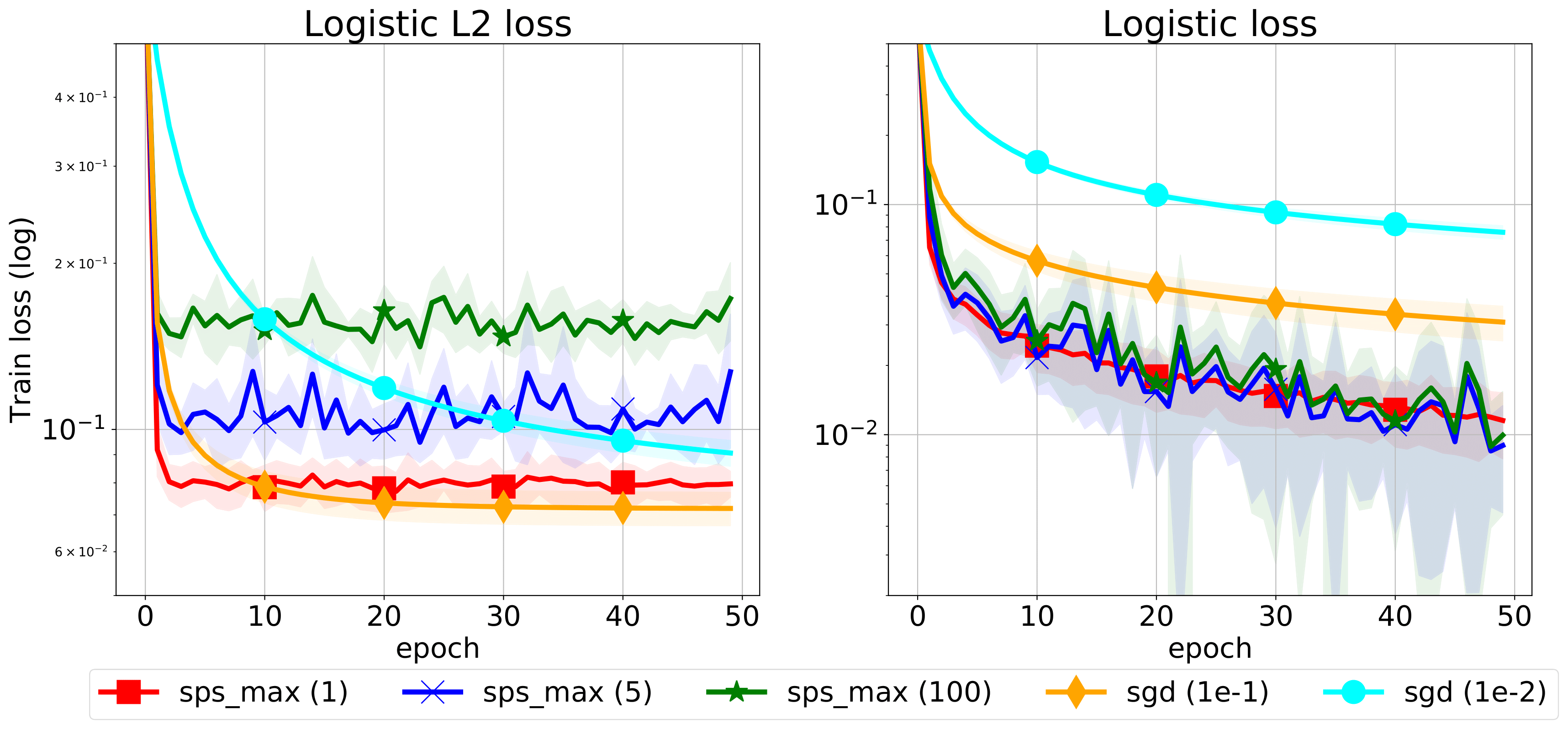
We propose a stochastic variant of the classical Polyak step-size (Polyak, 1987) commonly used in the subgradient method. Although computing the Polyak step-size requires knowledge of the optimal function values, this information is readily available for typical modern machine learning applications. Consequently, the proposed stochastic Polyak step-size (SPS) is an attractive choice for setting the learning rate for stochastic gradient descent (SGD). We provide theoretical convergence guarantees for SGD equipped with SPS in different settings, including strongly convex, convex and non-convex functions. Furthermore, our analysis results in novel convergence guarantees for SGD with a constant step-size. We show that SPS is particularly effective when training over-parameterized models capable of interpolating the training data. In this setting, we prove that SPS enables SGD to converge to the true solution at a fast rate without requiring the knowledge of any problem-dependent constants or additional computational overhead. We experimentally validate our theoretical results via extensive experiments on synthetic and real datasets. We demonstrate the strong performance of SGD with SPS compared to state-of-the-art optimization methods when training over-parameterized models.
翻译:我们提议了一个典型的Polyak梯度(Pollyak,1987年)的理论变体。虽然计算Polyak梯度需要了解最佳功能值的知识,但这一信息很容易用于典型的现代机器学习应用,因此,拟议的Sotchatic Polyak梯度(SPS)是确定随机梯度梯度下降的学习率的有吸引力的选择。我们为在不同环境中配备了SPS的SGD提供了理论趋同保证,包括强烈的凝固、凝固和非凝固功能。此外,我们的分析得出了SGD新颖的趋同保证,使SGD具有恒定的分级尺寸。我们表明,在培训能够对培训数据进行相互调试算的超分度模型时,SPSWA特别有效。在这种环境下,我们证明SPSM使SGD能够在不要求了解任何与问题相关的常数或额外的计算间接费用的情况下,以快速速速率求得一致。我们通过对合成和真实数据集的广泛试验来验证我们的理论结果。我们用SGDGD模型与SBM模型相比,在进行州制的优化方法上展示了强大的表现。