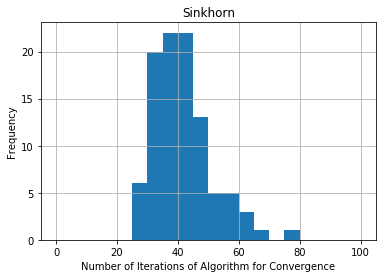
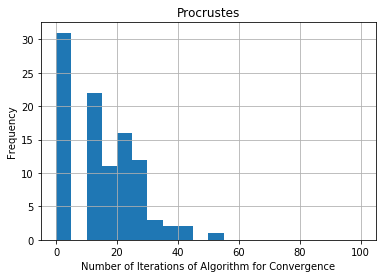
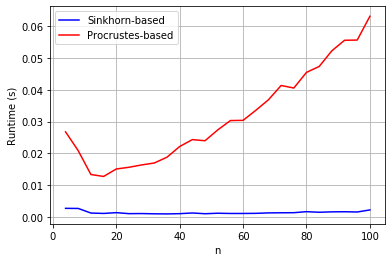
In this paper we study the problem of decomposing a given tensor into a tensor train such that the tensors at the vertices are orthogonally decomposable. When the tensor train has length two, and the orthogonally decomposable tensors at the two vertices are symmetric, we recover the decomposition by considering random linear combinations of slices. Furthermore, if the tensors at the vertices are symmetric and low-rank but not orthogonally decomposable, we show that a whitening procedure can transform the problem into the orthogonal case. When the tensor network has length three or more and the tensors at the vertices are symmetric and orthogonally decomposable, we provide an algorithm for recovering them subject to some rank conditions. Finally, in the case of tensor trains of length two in which the tensors at the vertices are orthogonally decomposable but not necessarily symmetric, we show that the decomposition problem reduces to the novel problem of decomposing a matrix into an orthogonal matrix multiplied by diagonal matrices on either side. We provide and compare two solutions, one based on Sinkhorn's theorem and one on Procrustes' algorithm. We conclude with a multitude of open problems in linear and multilinear algebra that arose in our study.
翻译:在本文中,我们研究将给定的电压分解成一个电压列的问题,这样,顶部的电压分解可以分解。当高压列的长度为2,而两个顶部的电压分解器是对称的,我们通过考虑切片随机线性组合来恢复分解。此外,如果顶部的电压分解是对称和低级的,但不会分解,那么,我们表明,白化程序可以将问题转化成正方形的情况。当高压列的长度为3或以上,而顶部的电压分解器是对称的,我们通过考虑随机线性切片组合来恢复分解的问题。最后,如果顶部的电压分解为两长的电压列,那么在我们脊椎的电压分解过程中,我们发现一个白程序可以将问题转换成多面的直线性矩阵,我们通过两个不同层次的解剖式矩阵研究,我们发现,一个分解式的解问题会通过一个分解到一个分解式的矩阵,一个分解到一个分解式的矩阵,一个分解到一个分解到一个分解到一个分解式的矩阵,然后在一个分解到一个分解到一个新的的矩阵。