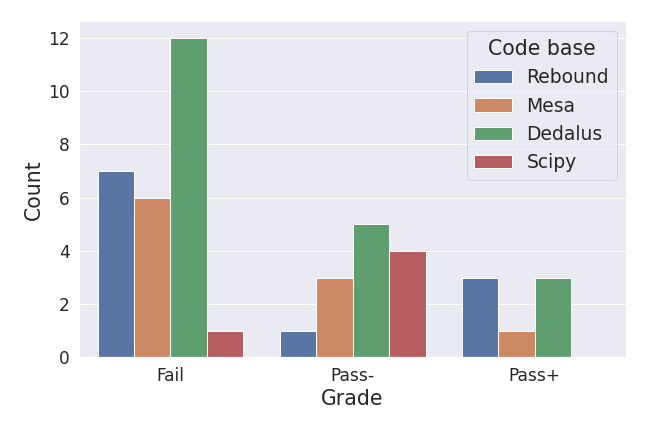
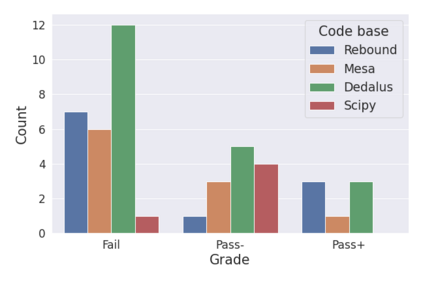
[Abridged abstract] Large Language Models (LLMs) can solve some undergraduate-level to graduate-level physics textbook problems and are proficient at coding. Combining these two capabilities could one day enable AI systems to simulate and predict the physical world. We present an evaluation of state-of-the-art (SOTA) LLMs on PhD-level to research-level computational physics problems. We condition LLM generation on the use of well-documented and widely-used packages to elicit coding capabilities in the physics and astrophysics domains. We contribute $\sim 50$ original and challenging problems in celestial mechanics (with REBOUND), stellar physics (with MESA), 1D fluid dynamics (with Dedalus) and non-linear dynamics (with SciPy). Since our problems do not admit unique solutions, we evaluate LLM performance on several soft metrics: counts of lines that contain different types of errors (coding, physics, necessity and sufficiency) as well as a more "educational" Pass-Fail metric focused on capturing the salient physical ingredients of the problem at hand. As expected, today's SOTA LLM (GPT4) zero-shot fails most of our problems, although about 40\% of the solutions could plausibly get a passing grade. About $70-90 \%$ of the code lines produced are necessary, sufficient and correct (coding \& physics). Physics and coding errors are the most common, with some unnecessary or insufficient lines. We observe significant variations across problem class and difficulty. We identify several failure modes of GPT4 in the computational physics domain. Our reconnaissance work provides a snapshot of current computational capabilities in classical physics and points to obvious improvement targets if AI systems are ever to reach a basic level of autonomy in physics simulation capabilities.
翻译:暂无翻译