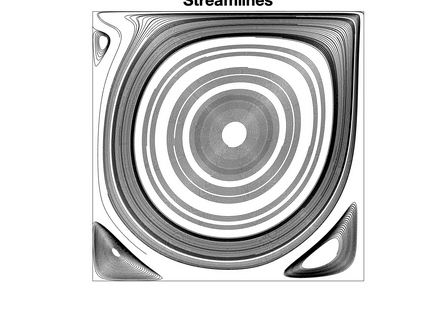
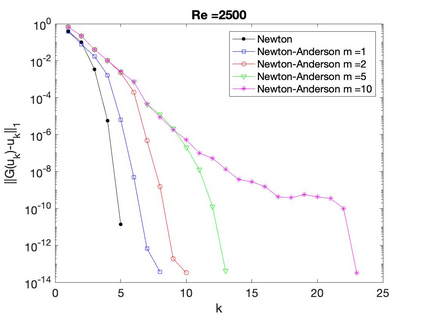
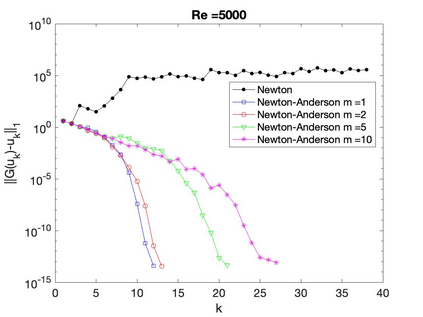
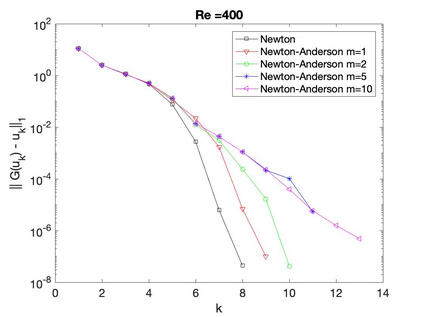
This paper studies the performance Newton's iteration applied with Anderson acceleration for solving the incompressible steady Navier-Stokes equations. We manifest that this method converges superlinearly with a good initial guess, and moreover, a large Anderson depth decelerates the convergence speed comparing to a small Anderson depth. We observe that the numerical tests confirm these analytical convergence results, and in addition, Anderson acceleration sometimes enlarges the domain of convergence for Newton's method.
翻译:本文研究牛顿的性能迭代与安德森加速法用于解决不可压缩的稳态纳维尔-斯托克斯方程式。 我们发现这种方法与一个良好的初步猜测相融合,此外,与一个小的安德森深度相比,一个大的安德森深度使趋同速度减速。我们观察到,数字测试证实了这些分析趋同结果,此外,安德森加速法有时会扩大牛顿法的趋同范围。
相关内容
专知会员服务
36+阅读 · 2019年10月17日
Arxiv
0+阅读 · 2022年4月20日
Arxiv
0+阅读 · 2022年4月19日
Arxiv
1+阅读 · 2022年4月18日
Arxiv
0+阅读 · 2022年4月17日