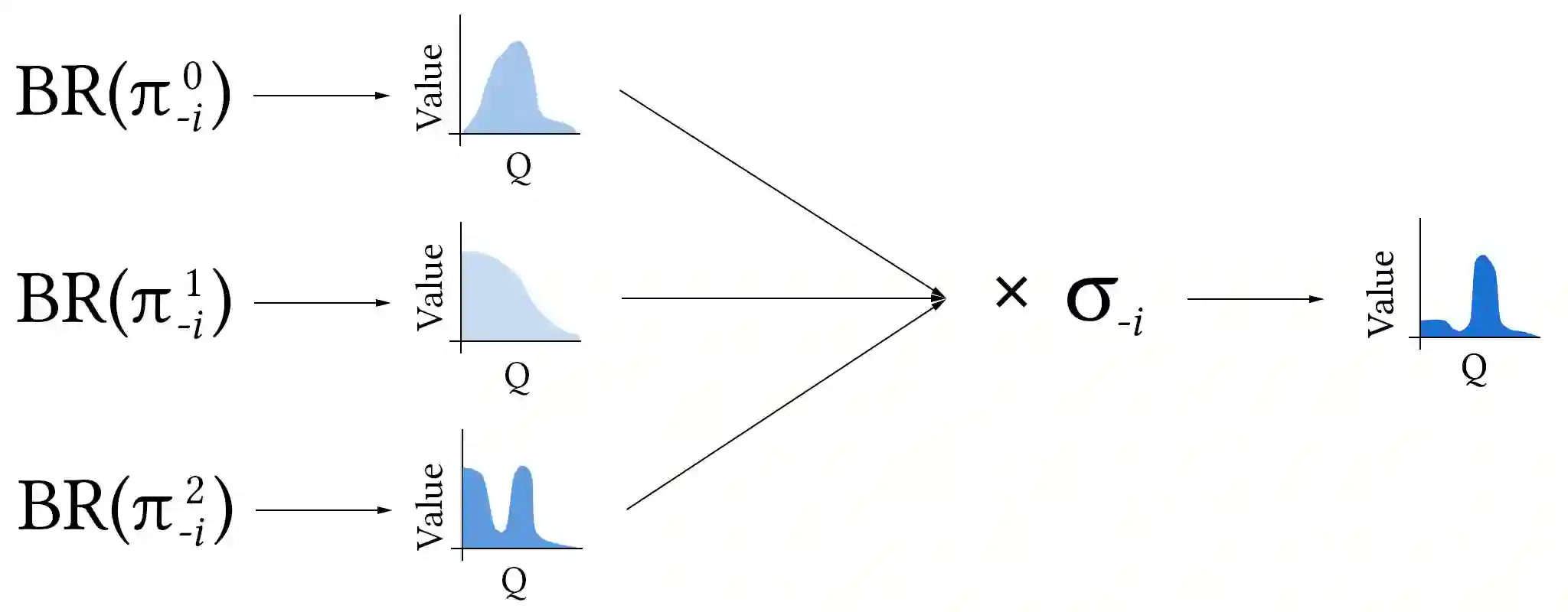
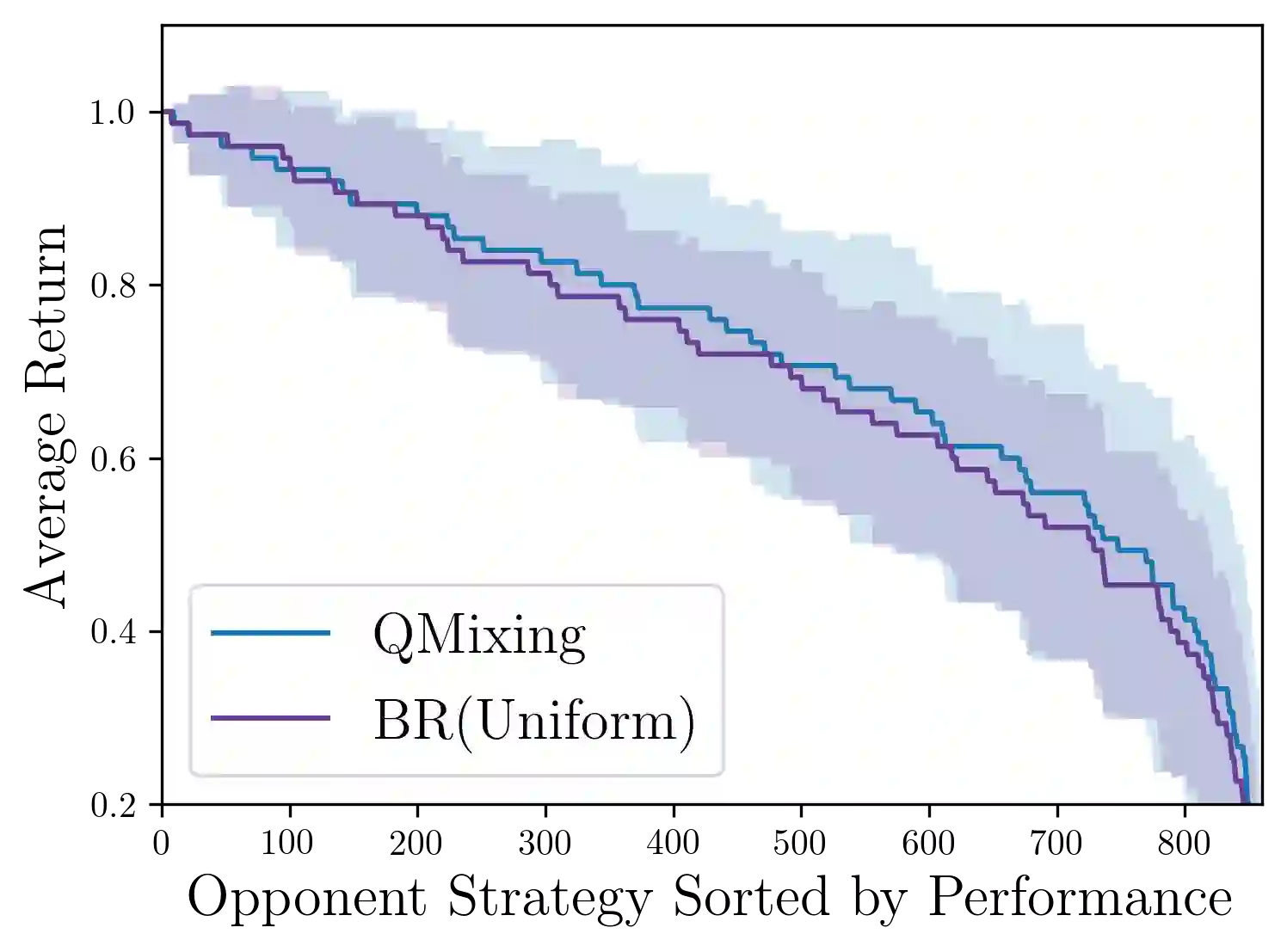
Intuitively, experience playing against one mixture of opponents in a given domain should be relevant for a different mixture in the same domain. We propose a transfer learning method, Q-Mixing, that starts by learning Q-values against each pure-strategy opponent. Then a Q-value for any distribution of opponent strategies is approximated by appropriately averaging the separately learned Q-values. From these components, we construct policies against all opponent mixtures without any further training. We empirically validate Q-Mixing in two environments: a simple grid-world soccer environment, and a complicated cyber-security game. We find that Q-Mixing is able to successfully transfer knowledge across any mixture of opponents. We next consider the use of observations during play to update the believed distribution of opponents. We introduce an opponent classifier -- trained in parallel to Q-learning, using the same data -- and use the classifier results to refine the mixing of Q-values. We find that Q-Mixing augmented with the opponent classifier function performs comparably, and with lower variance, than training directly against a mixed-strategy opponent.
翻译:直观地说, 对抗某个域内反对者的一种混合物的经验应该与同一域内不同的混合物相关。 我们建议一种转移学习方法, 即 Q- 混合, 以学习对每个纯战略对手的Q值为起点。 然后, 任何对手战略的分布的Q值, 都可以通过适当平均单独学习的Q值来近似。 我们从这些组成部分中, 制定针对所有对手混合物的政策, 无需经过任何进一步的培训 。 我们从经验上验证 Q- 混合 在两个环境中: 一个简单的网格- 世界足球环境, 一个复杂的网络安全游戏。 我们发现 Q- 混合能够成功地在任何反对者的混合中转让知识。 我们接下来考虑在游戏中使用观察来更新反对者相信的分布 。 我们引入一个反对者分类器 -- 与Q- 学习平行训练, 使用同样的数据 -- 并使用分类结果来改进Q- 价值的混合。 我们发现 Q- 混合混合混合组合与对手分类功能相匹配, 差异小于直接训练 。