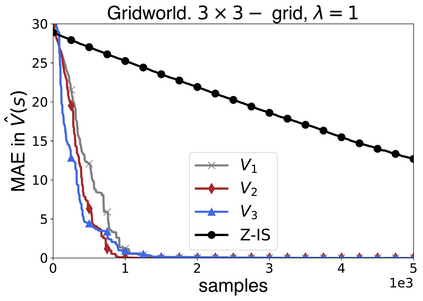
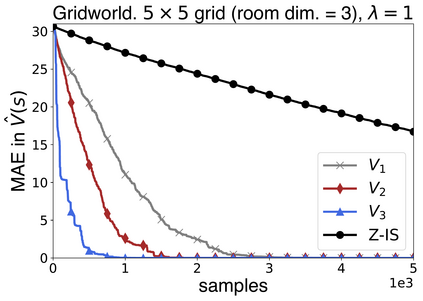
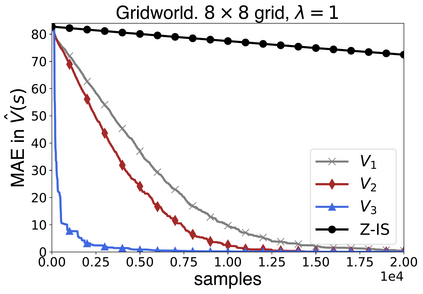
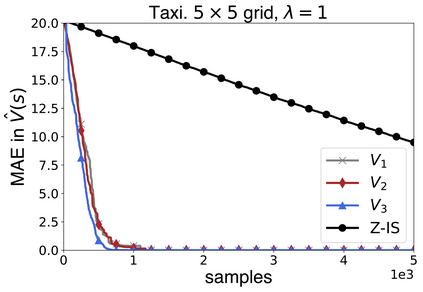
In this work we present a novel approach to hierarchical reinforcement learning for linearly-solvable Markov decision processes. Our approach assumes that the state space is partitioned, and the subtasks consist in moving between the partitions. We represent value functions on several levels of abstraction, and use the compositionality of subtasks to estimate the optimal values of the states in each partition. The policy is implicitly defined on these optimal value estimates, rather than being decomposed among the subtasks. As a consequence, our approach can learn the globally optimal policy, and does not suffer from the non-stationarity of high-level decisions. If several partitions have equivalent dynamics, the subtasks of those partitions can be shared. If the set of boundary states is smaller than the entire state space, our approach can have significantly smaller sample complexity than that of a flat learner, and we validate this empirically in several experiments.
翻译:在这项工作中,我们为线性溶解的Markov 决策进程提出了一个等级强化学习的新方法。 我们的方法假定国家空间被分割,子任务在于分割。 我们代表了数级抽象的值函数, 并使用子任务的组成性来估计每个分割区国家的最佳值。 政策以这些最佳值估计为暗含的定义, 而不是在子任务中分解。 因此, 我们的方法可以学习全球最佳政策, 并且不会因为高级决定的不固定性而受到影响。 如果几个分区具有等效的动态, 这些分区的子任务可以共享。 如果一组边界国家小于整个国家空间, 我们的方法的样本复杂性可以大大小于平板学习者, 我们在几个实验中也证实了这一点。