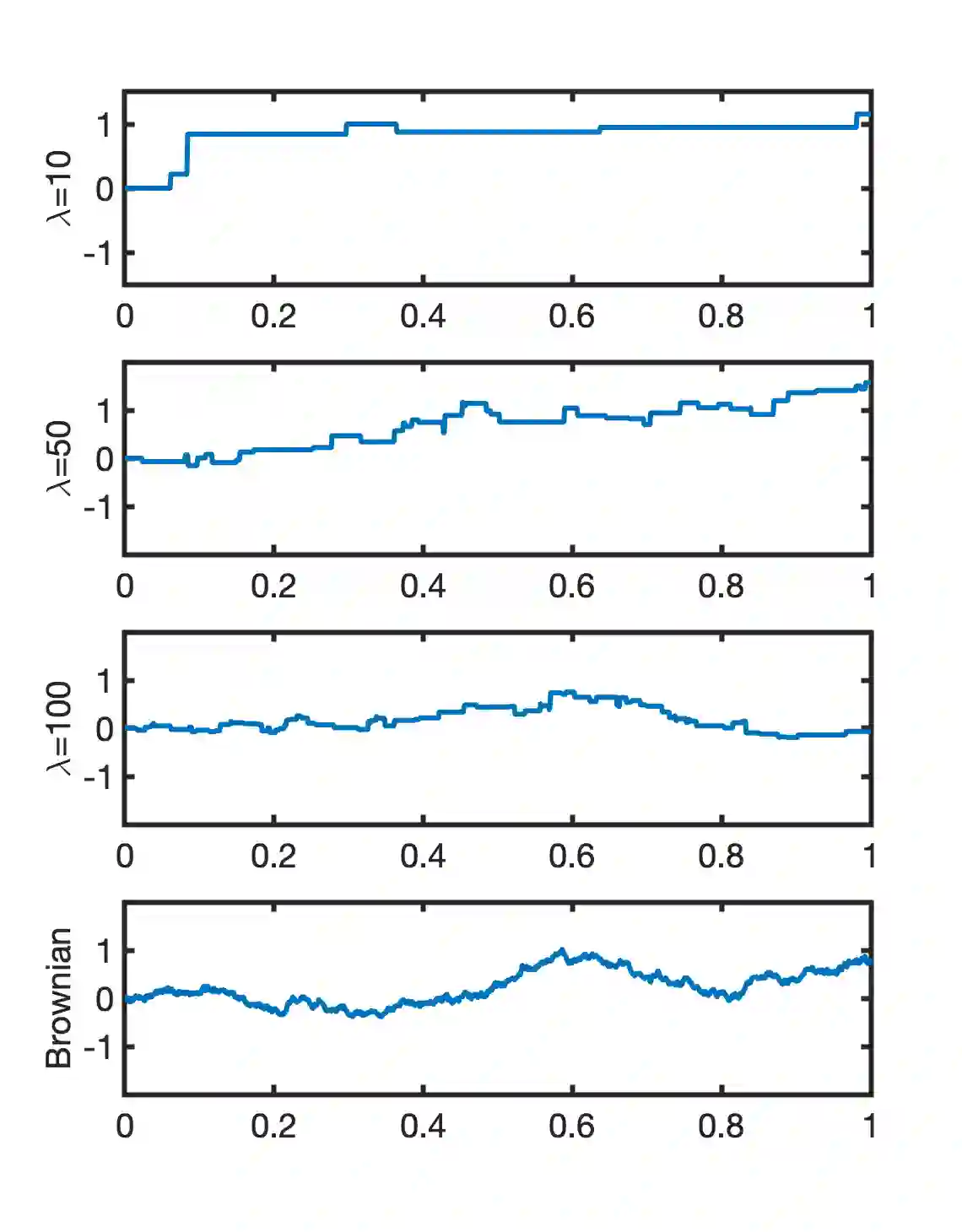
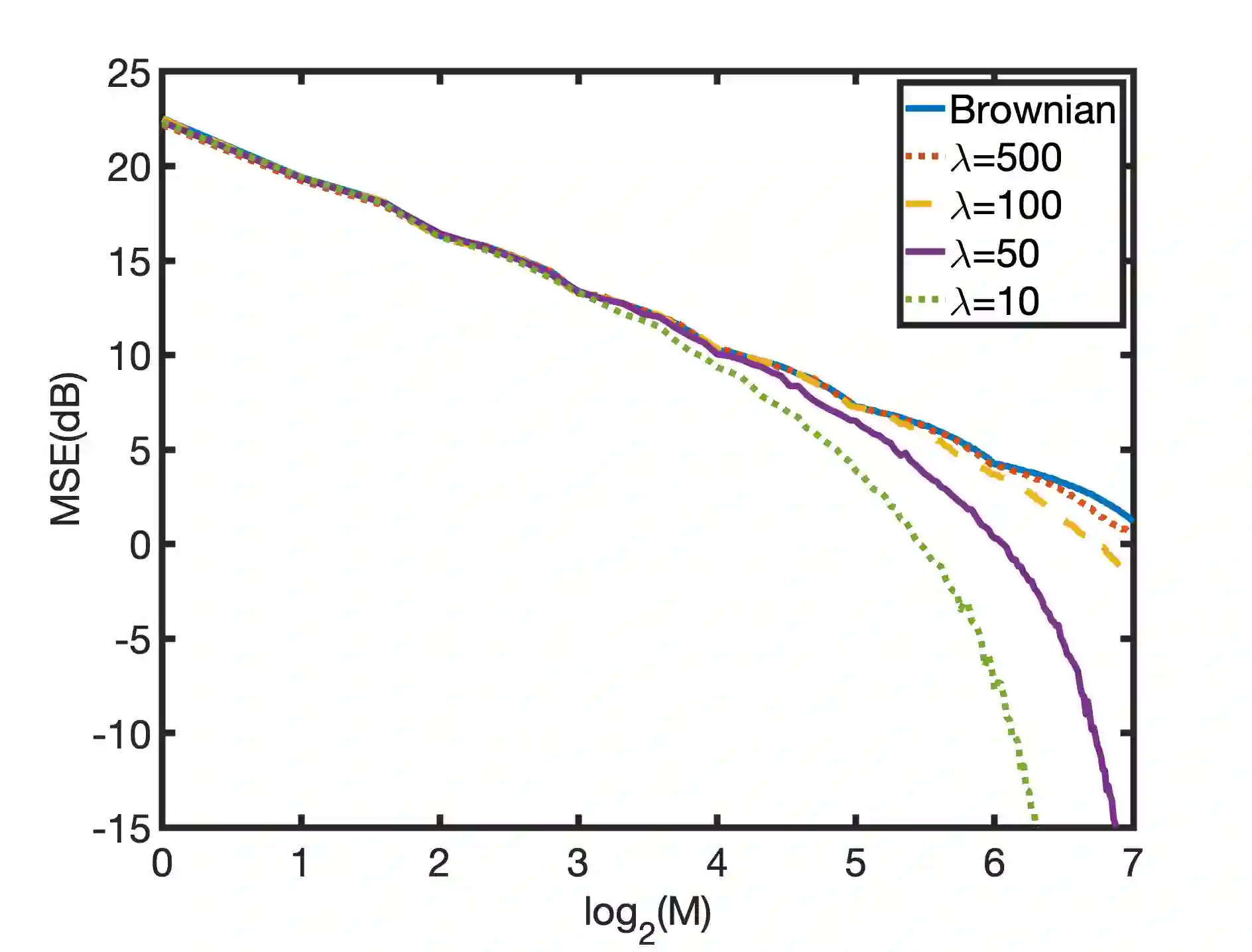
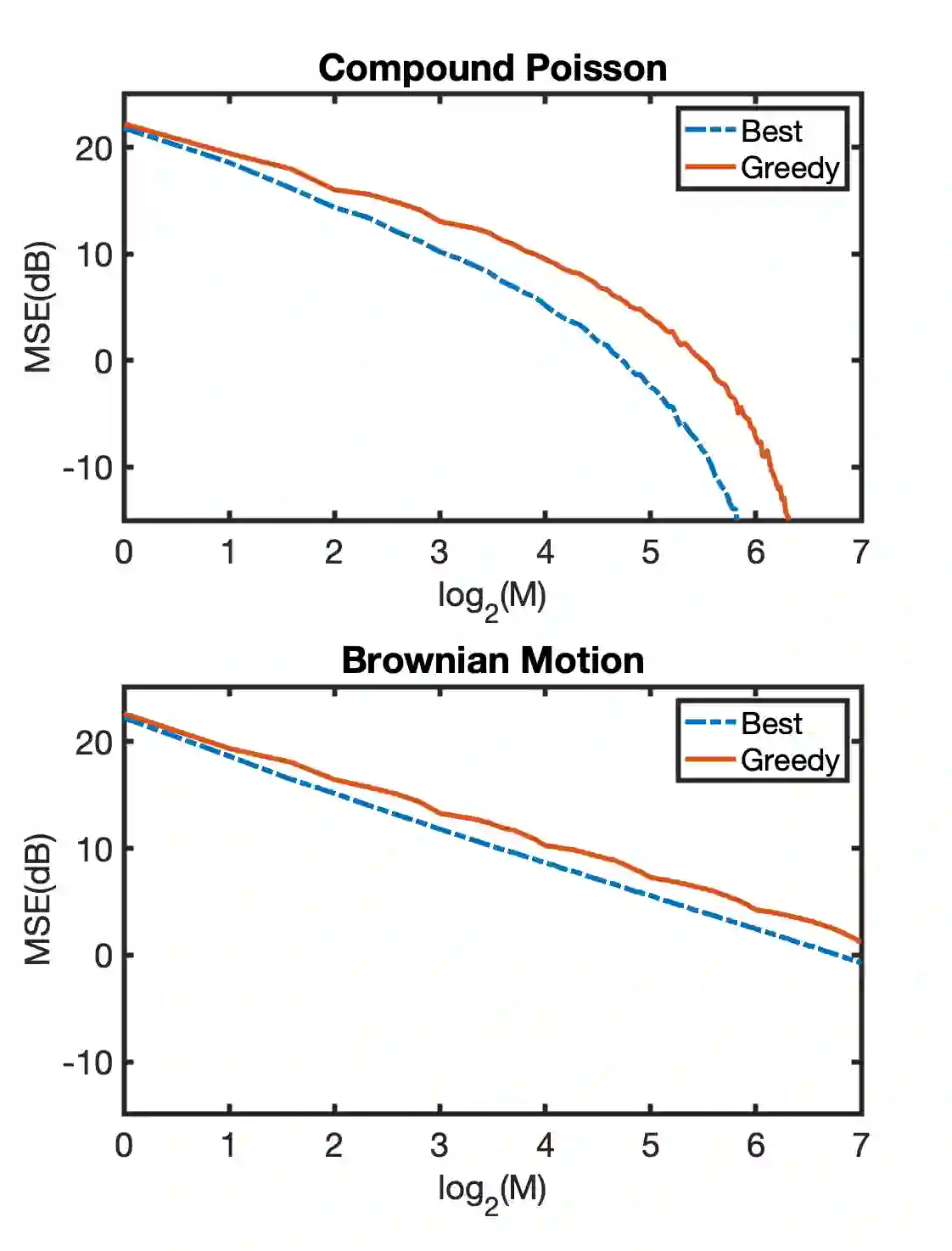
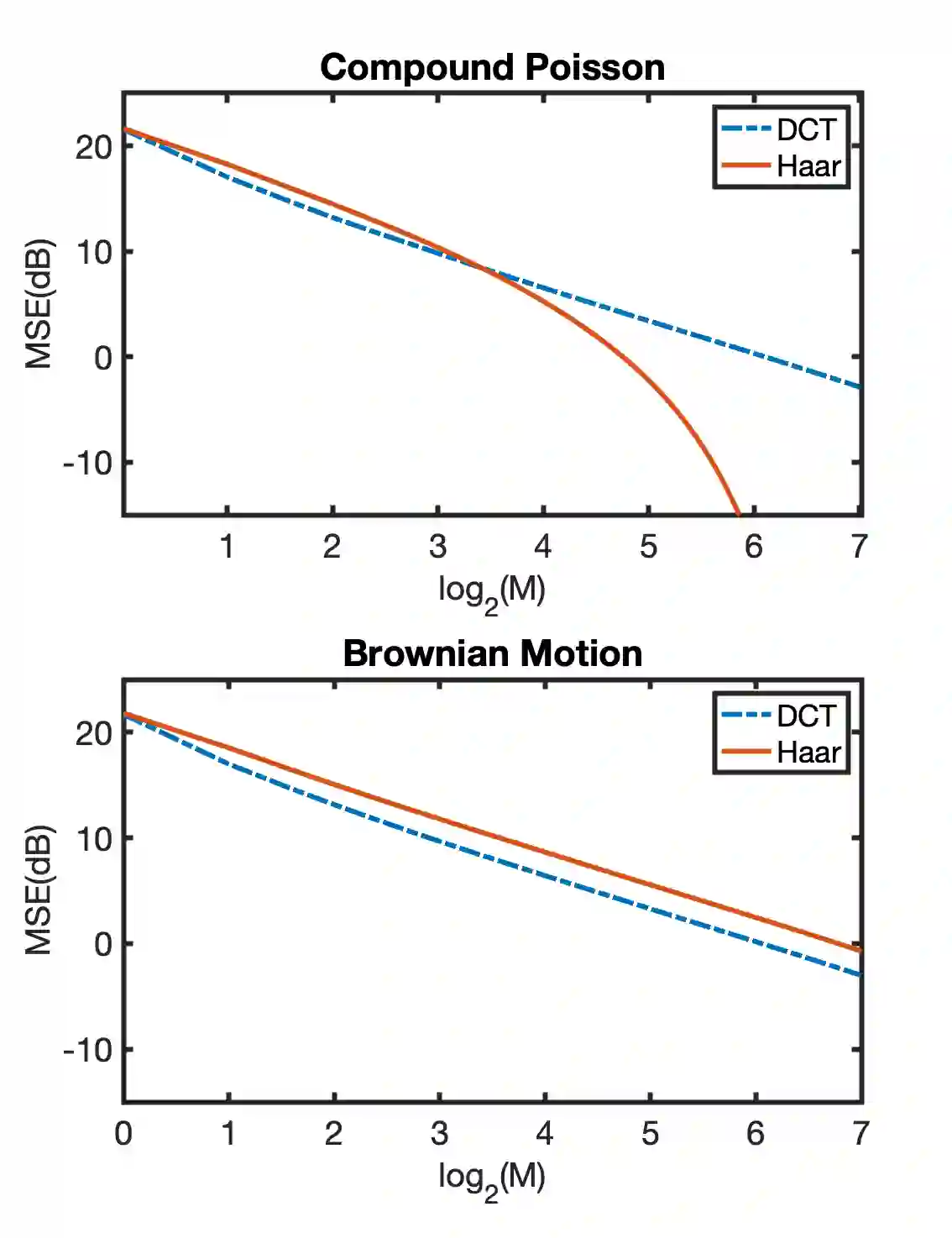
In this paper, we precisely quantify the wavelet compressibility of compound Poisson processes. To that end, we expand the given random process over the Haar wavelet basis and we analyse its asymptotic approximation properties. By only considering the nonzero wavelet coefficients up to a given scale, what we call the greedy approximation, we exploit the extreme sparsity of the wavelet expansion that derives from the piecewise-constant nature of compound Poisson processes. More precisely, we provide lower and upper bounds for the mean squared error of greedy approximation of compound Poisson processes. We are then able to deduce that the greedy approximation error has a sub-exponential and super-polynomial asymptotic behavior. Finally, we provide numerical experiments to highlight the remarkable ability of wavelet-based dictionaries in achieving highly compressible approximations of compound Poisson processes.
翻译:在本文中, 我们精确地量化了 复合 Poisson 过程的波浪压缩。 为此, 我们将给定的随机过程扩展到 Haar 波浪基底, 并分析其无症状近似特性。 我们仅仅考虑到非零波子系数, 最高可达给定规模, 我们称之为贪婪近似, 我们利用波浪膨胀的极端偏狭性, 其来源于复合 Poisson 过程的片断性。 更准确地说, 我们为化合物 Poisson 进程贪婪近似的平均正方差错误提供了下限和上限。 然后我们可以推断出贪婪近似错误具有亚为耗尽性和超极极极极极极极极无药性行为。 最后, 我们提供数字实验, 以突出基于波浪的字典在达到复合 Poisson 过程的高度可压缩近比值方面的巨大能力 。