Three ways that non-differentiability affects neural network training

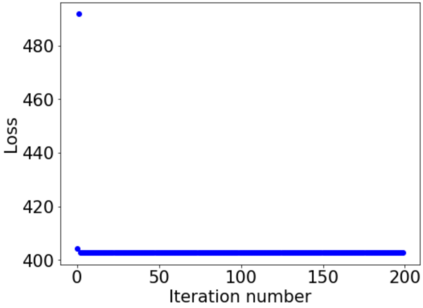
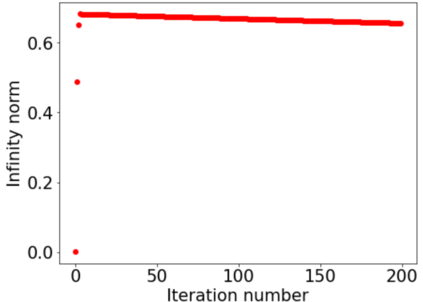
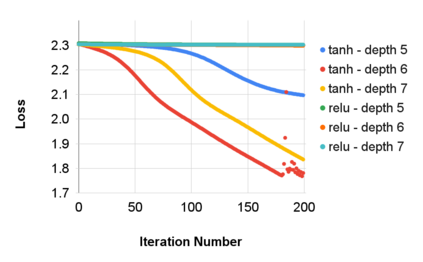
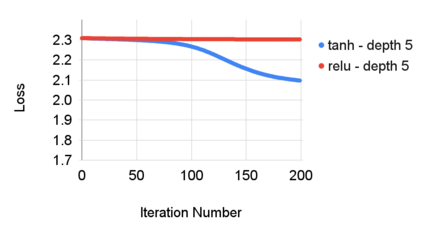
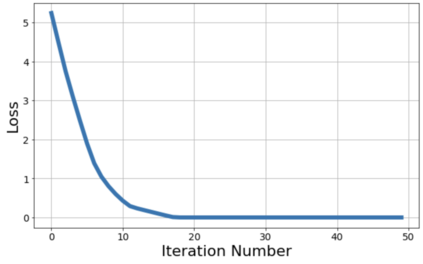
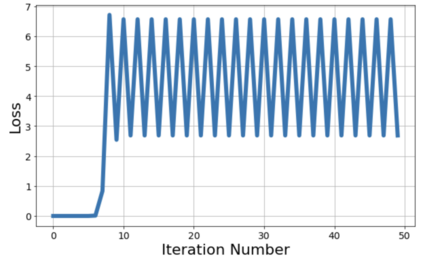
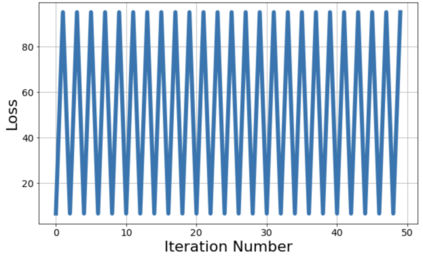
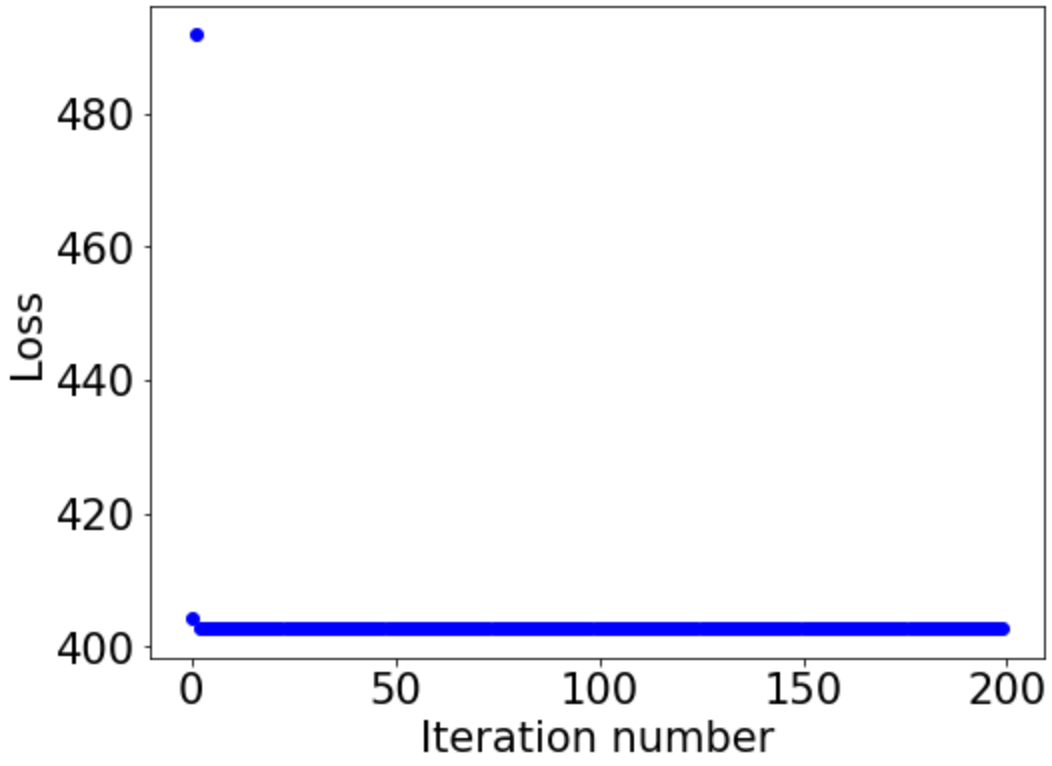
This paper investigates how non-differentiability affects three different aspects of the neural network training process. We first analyze fully connected neural networks with ReLU activations, for which we show that the continuously differentiable neural networks converge faster than non-differentiable neural networks. Next, we analyze the problem of $L_{1}$ regularization and show that the solutions produced by deep learning solvers are incorrect and counter-intuitive even for the $L_{1}$ penalized linear model. Finally, we analyze the Edge of Stability problem, where we show that all convex, non-smooth, Lipschitz continuous functions display unstable convergence, and provide an example of a result derived using twice differentiable functions which fails in the once differentiable setting. More generally, our results suggest that accounting for the non-linearity of neural networks in the training process is essential for us to develop better algorithms, and to get a better understanding of the training process in general.