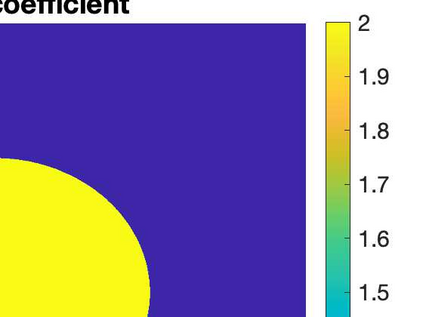
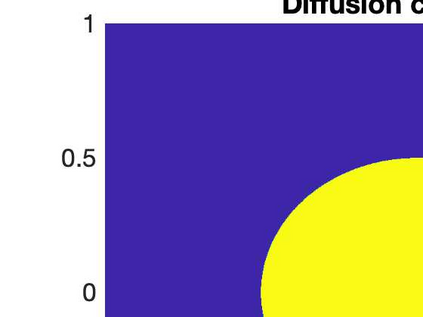
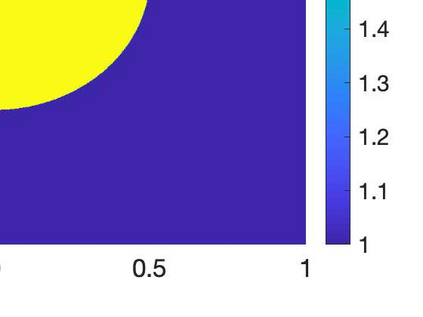
This paper is interested in developing reduced order models (ROMs) for repeated simulation of fractional elliptic partial differential equations (PDEs) for multiple values of the parameters (e.g., diffusion coefficients or fractional exponent) governing these models. These problems arise in many applications including simulating Gaussian processes, and geophysical electromagnetics. The approach uses the Kato integral formula to express the solution as an integral involving the solution of a parametrized elliptic PDE, which is discretized using finite elements in space and sinc quadrature for the fractional part. The offline stage of the ROM is accelerated using a solver for shifted linear systems, MPGMRES-Sh, and using a randomized approach for compressing the snapshot matrix. Our approach is both computational and memory efficient. Numerical experiments on a range of model problems, including an application to Gaussian processes, show the benefits of our approach.
翻译:暂无翻译