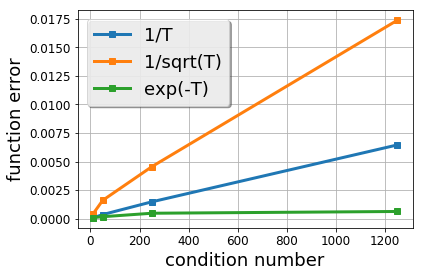
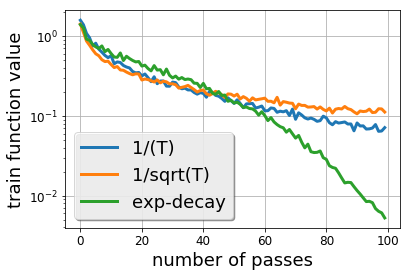
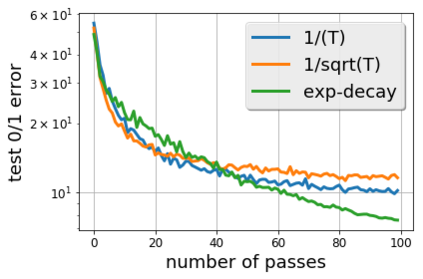
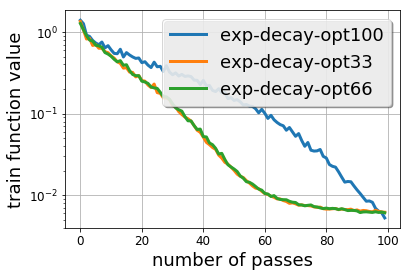
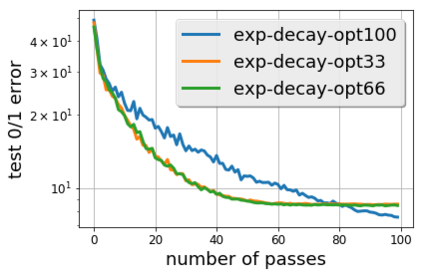
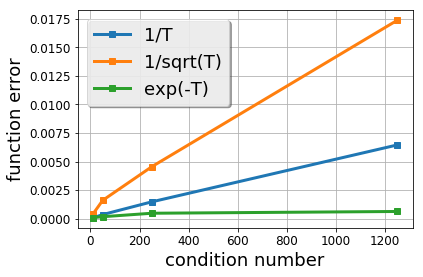
There is a stark disparity between the step size schedules used in practical large scale machine learning and those that are considered optimal by the theory of stochastic approximation. In theory, most results utilize polynomially decaying learning rate schedules, while, in practice, the "Step Decay" schedule is among the most popular schedules, where the learning rate is cut every constant number of epochs (i.e. this is a geometrically decaying schedule). This work examines the step-decay schedule for the stochastic optimization problem of streaming least squares regression (both in the non-strongly convex and strongly convex case), where we show that a sharp theoretical characterization of an optimal learning rate schedule is far more nuanced than suggested by previous work. We focus specifically on the rate that is achievable when using the final iterate of stochastic gradient descent, as is commonly done in practice. Our main result provably shows that a properly tuned geometrically decaying learning rate schedule provides an exponential improvement (in terms of the condition number) over any polynomially decaying learning rate schedule. We also provide experimental support for wider applicability of these results, including for training modern deep neural networks.
翻译:实际大规模机器学习中使用的职级规模表与实际大规模机器学习中采用的最优近似理论认为最优的职级表之间有着明显的差异。理论上,大多数成果都采用多学制衰减学习率表,而在实践中,“标准衰减”表是最受欢迎的时间表之一,在这种时间表中,学习率削减了每个恒定的时数(即,这是一个几何衰减时间表)。这项工作审查了流出的最小正方块回归(非强性convex和强性convex案例)的随机优化问题的职级表。在这种情况下,我们显示,对最佳学习率表的尖锐理论定性比以往工作所建议的要多得多。我们具体侧重于在使用随机梯度梯度梯度脱落最终值时能够实现的比率,这是实践中常见的做法。我们的主要结果可证实地表明,适当调整的几何级衰减学习率表(条件数)为任何多学系衰减的现代学习率网络提供了指数性改进(包括神经衰减率),我们还为这些较广的现代学习率提供实验性支持。