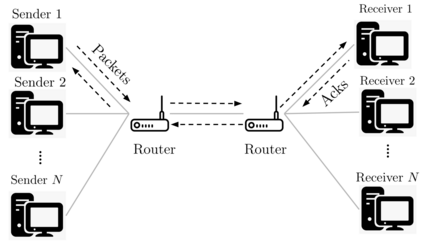
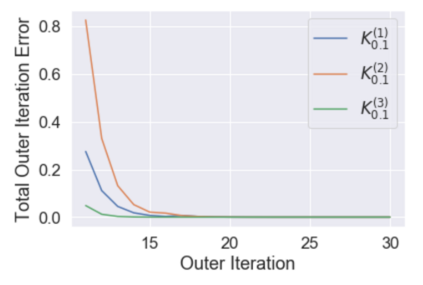
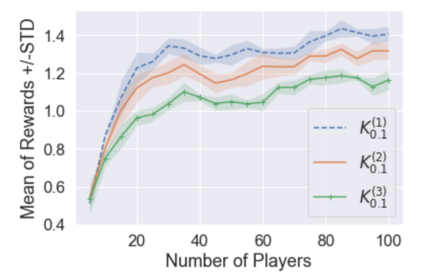
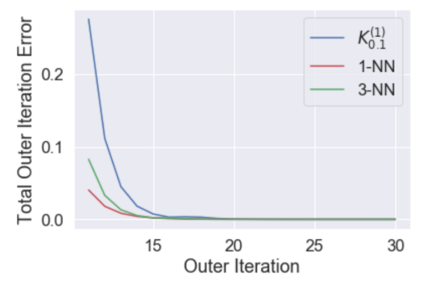
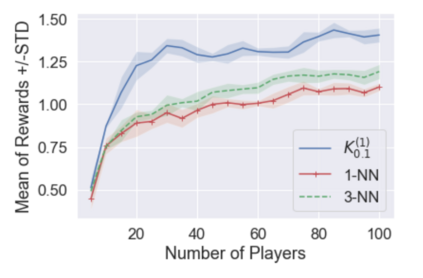
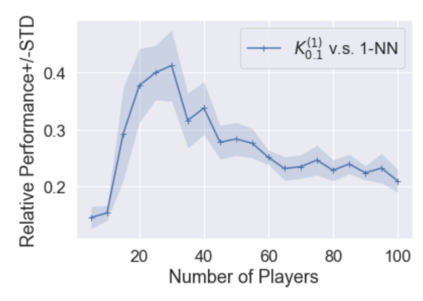
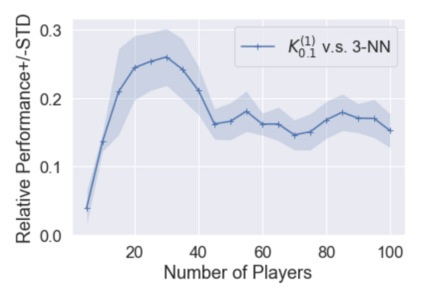
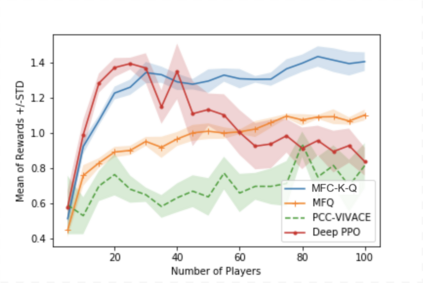
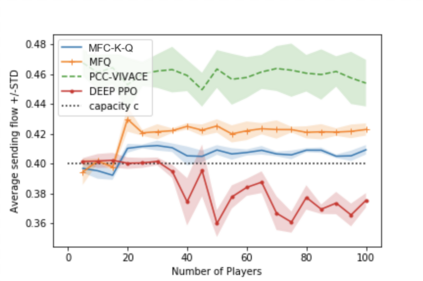
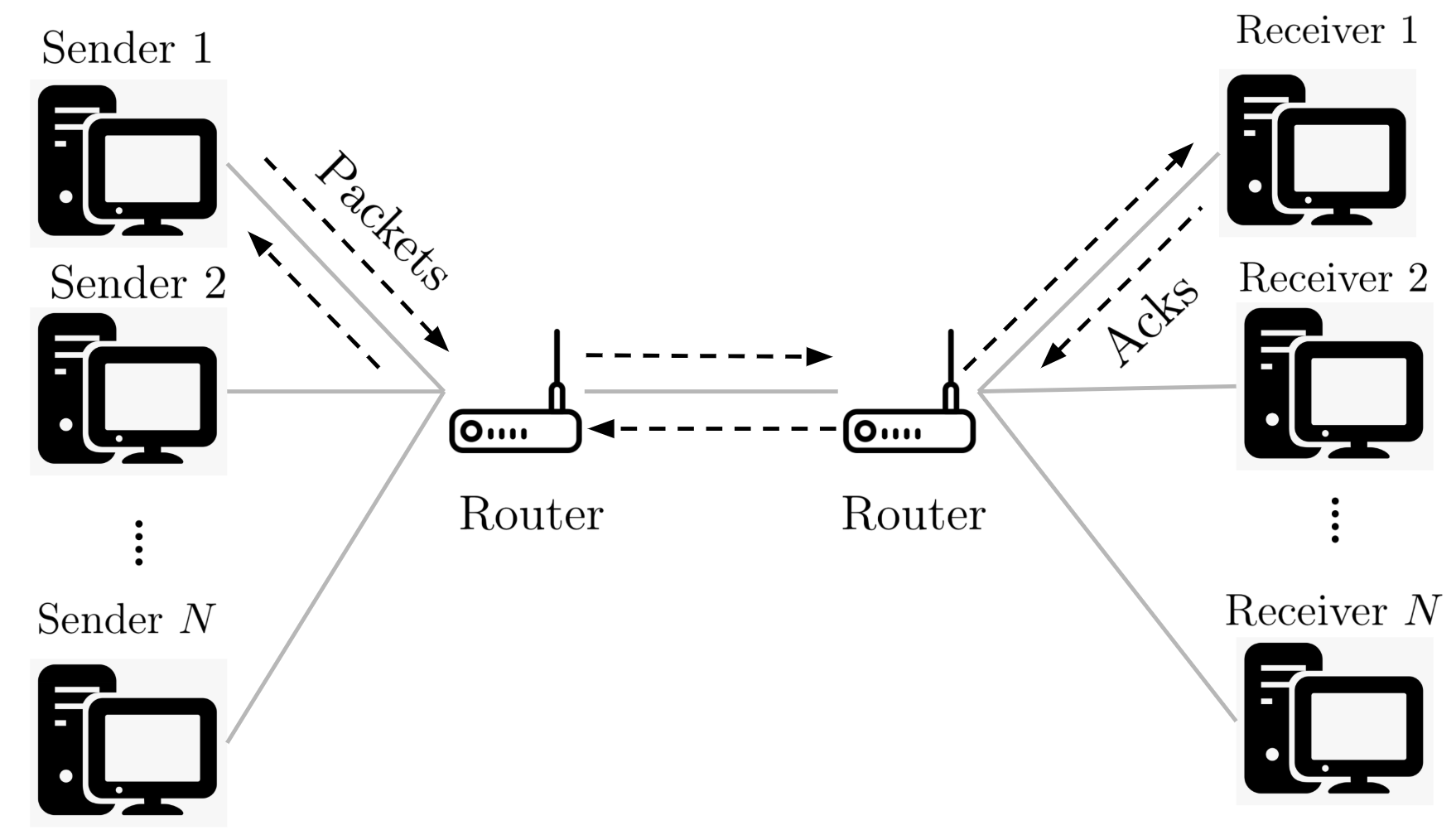
Multi-agent reinforcement learning (MARL), despite its popularity and empirical success, suffers from the curse of dimensionality. This paper builds the mathematical framework to approximate cooperative MARL by a mean-field control (MFC) approach, and shows that the approximation error is of $\mathcal{O}(\frac{1}{\sqrt{N}})$. By establishing an appropriate form of the dynamic programming principle for both the value function and the Q function, it proposes a model-free kernel-based Q-learning algorithm (MFC-K-Q), which is shown to have a linear convergence rate for the MFC problem, the first of its kind in the MARL literature. It further establishes that the convergence rate and the sample complexity of MFC-K-Q are independent of the number of agents $N$, which provides an $\mathcal{O}(\frac{1}{\sqrt{N}})$ approximation to the MARL problem with $N$ agents in the learning environment. Empirical studies for the network traffic congestion problem demonstrate that MFC-K-Q outperforms existing MARL algorithms when $N$ is large, for instance when $N>50$.
翻译:多剂强化学习(MARL)尽管广受欢迎,也取得了成功,但却受到多元性的诅咒。本文构建了数学框架,以中场控制(MRC)法来将合作MARL(MFC)近似于合作MARL(MFC),并显示近似误差为$mathcal{O}(\frac{1unsqrt{N ⁇ }}(frac{1unsqrt{N ⁇ )美元。通过为价值函数和Q函数建立适当的动态编程原则形式,它提议了一种无模型内核Q-学习算法(MFC-K-Q),该算法显示MFC问题的线性趋同率是MFC-K-Q在MARL文献中首例的趋同率。它进一步确定MFC-K-Q的趋同率和样本复杂度独立于代理商数量$N$(fCFC-K-Q)以外的代理商,而现有的MAL算法则是大时MFC-50美元。