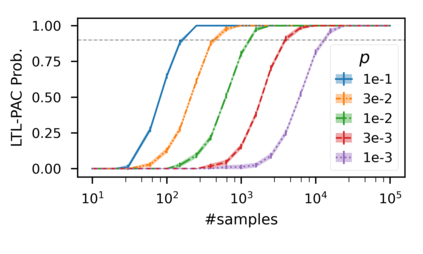
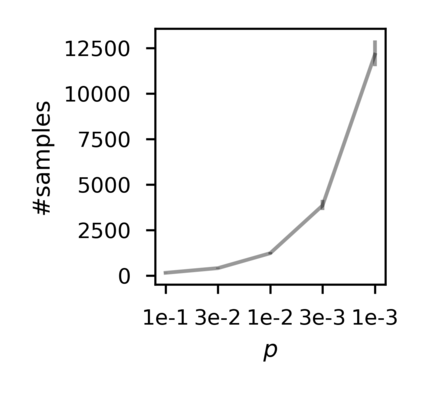
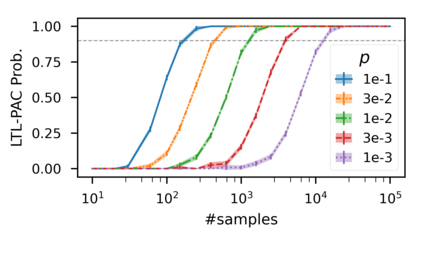
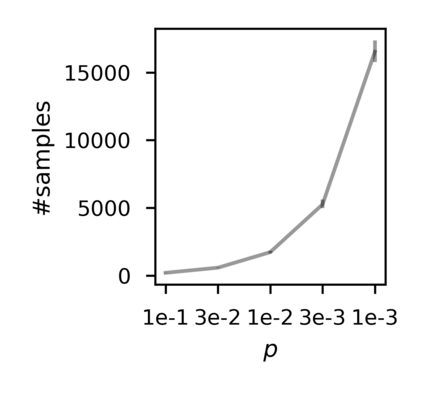
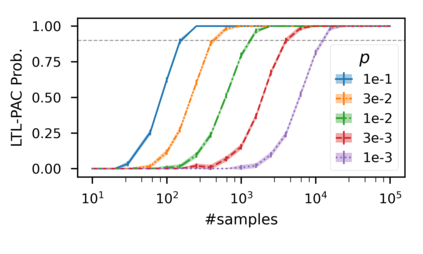
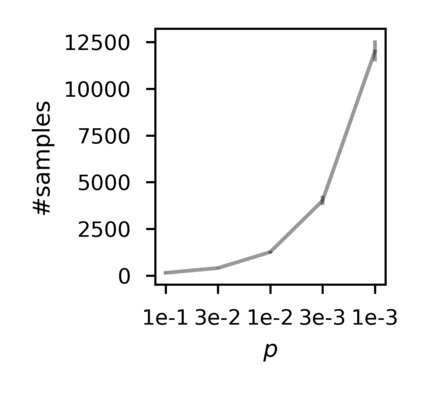
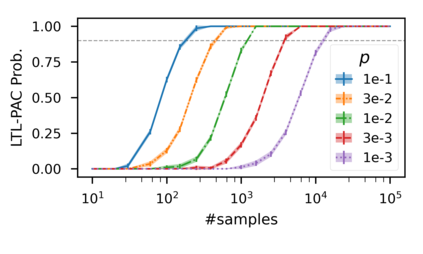
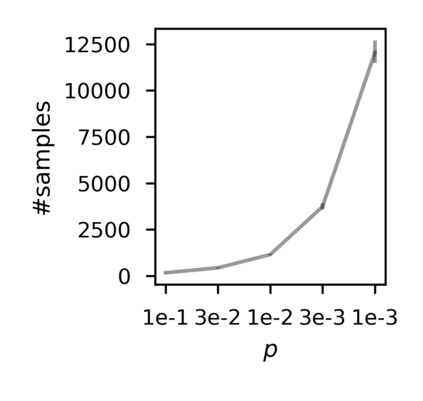
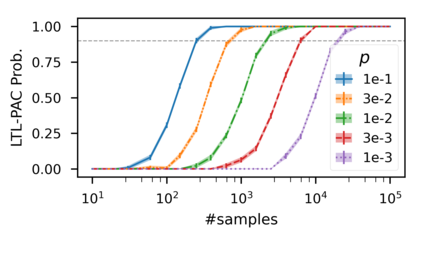
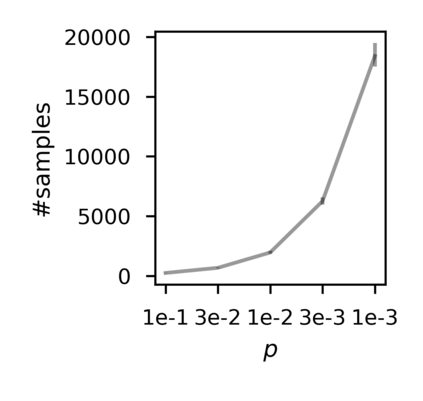
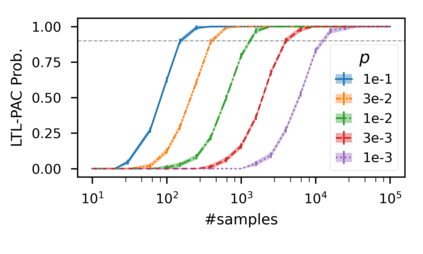
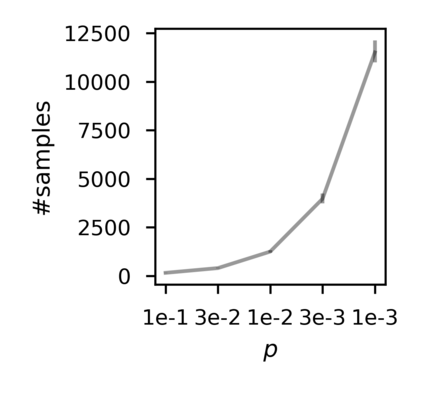
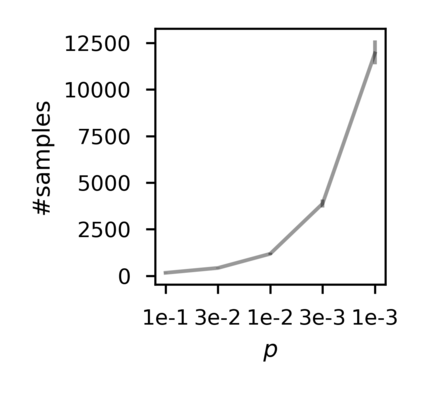
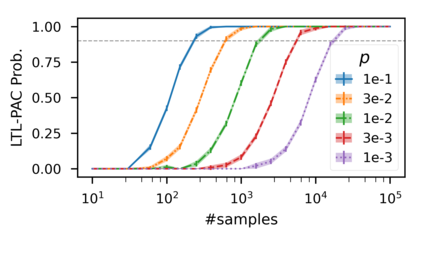
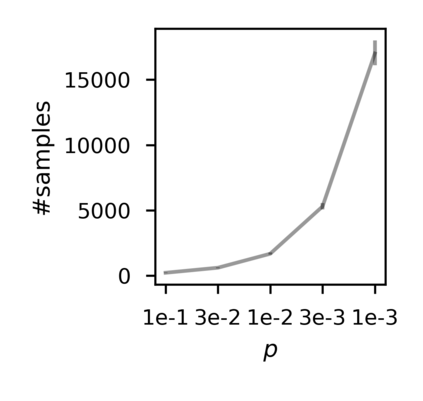
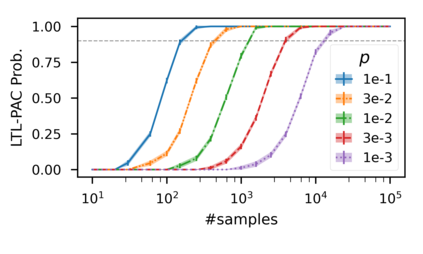
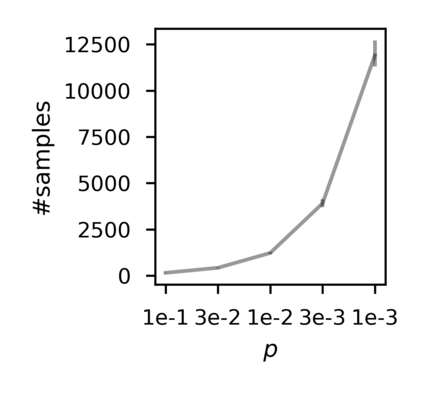
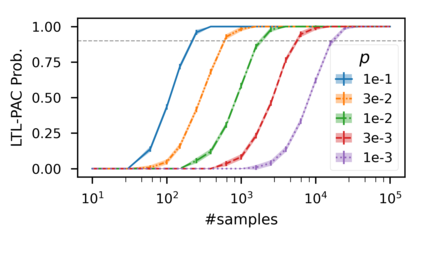
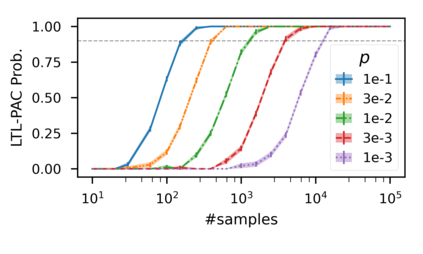
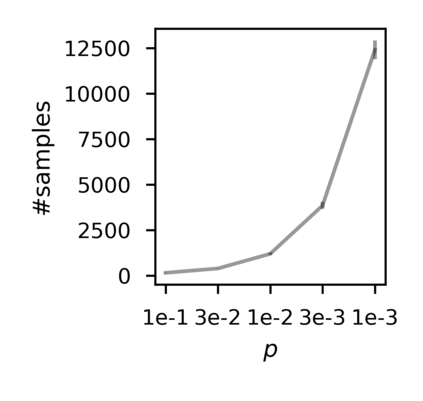
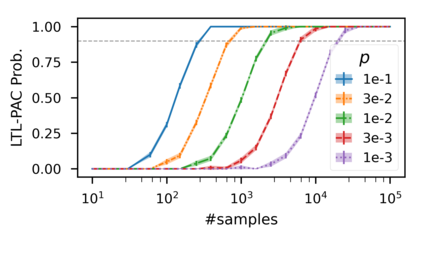
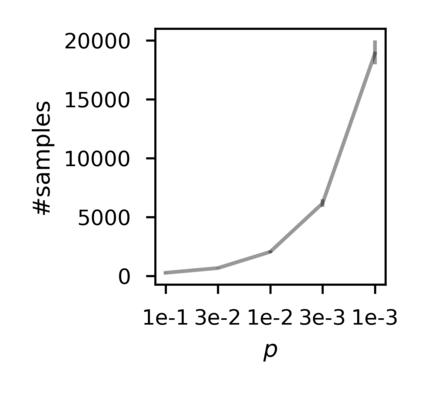
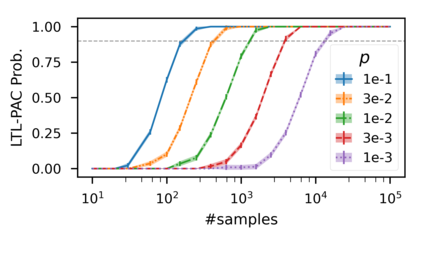
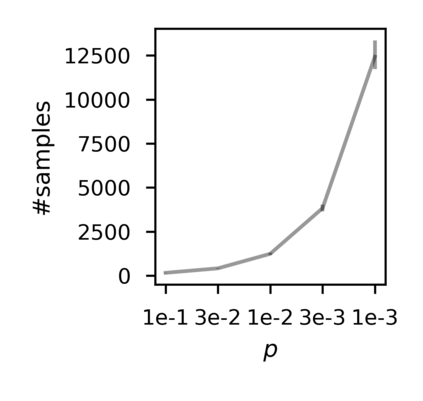
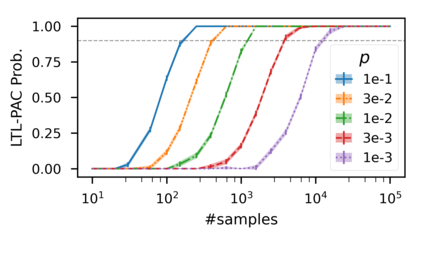
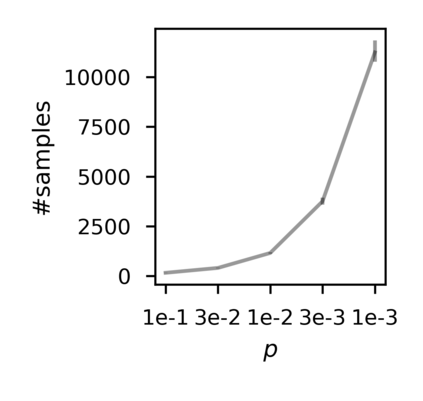
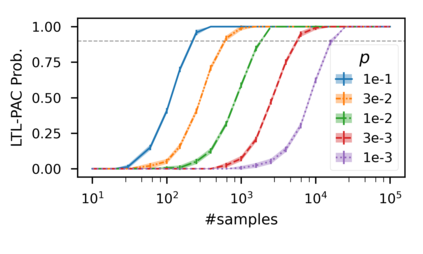
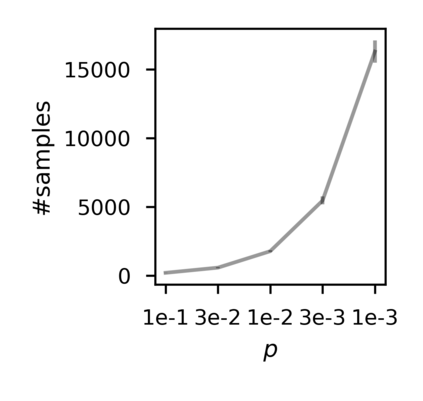
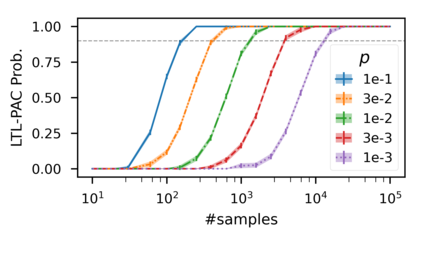
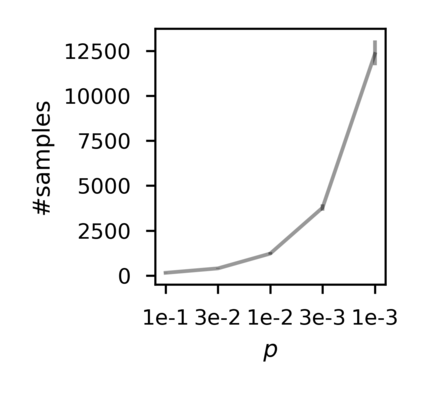
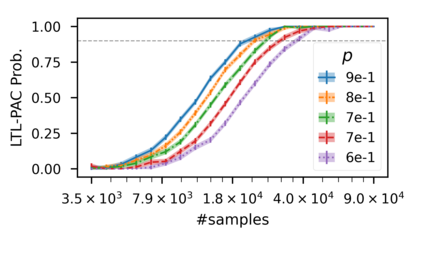
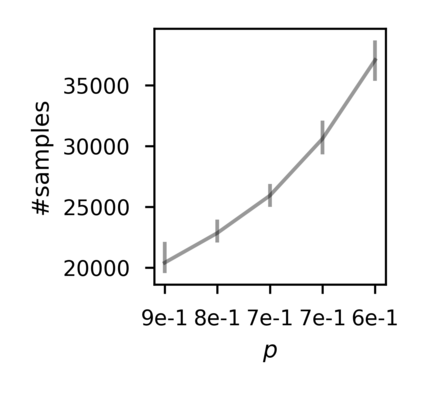
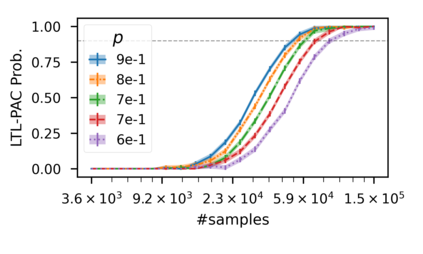
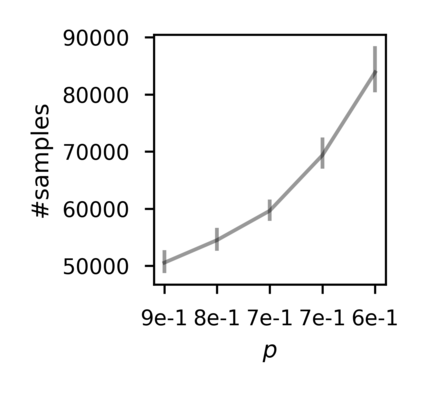
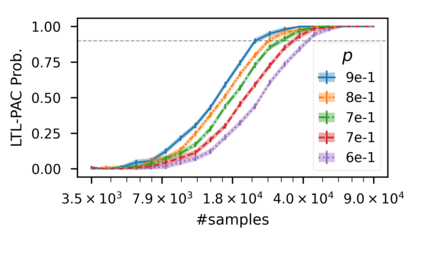
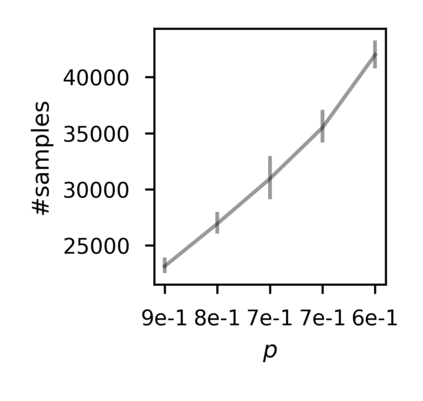
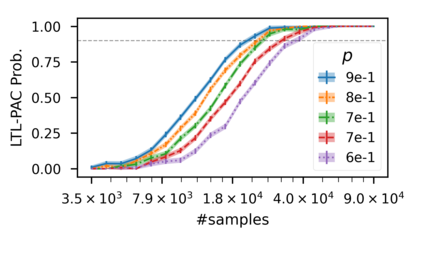
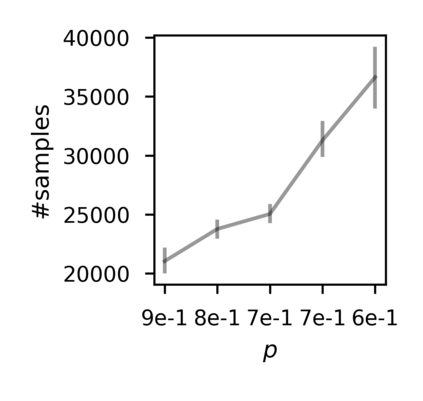
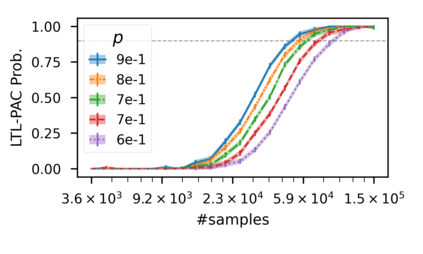
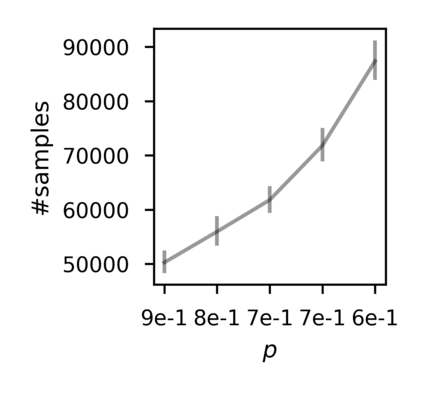
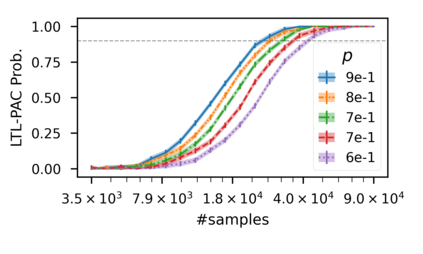
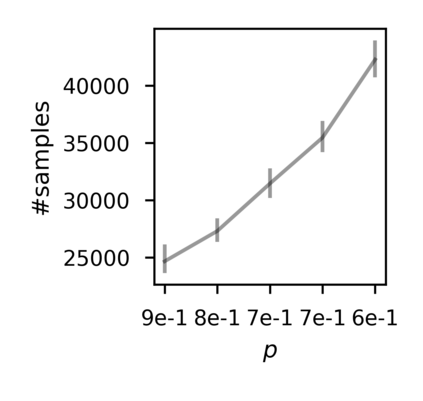
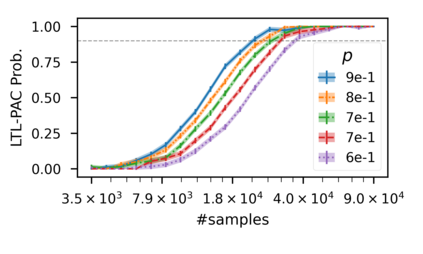
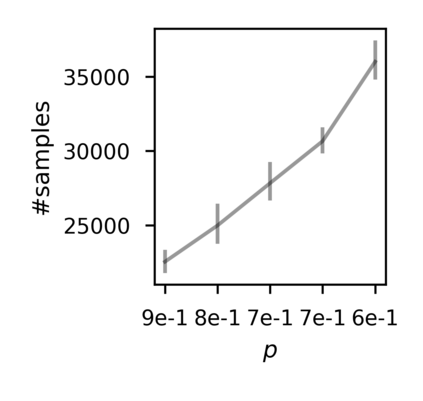
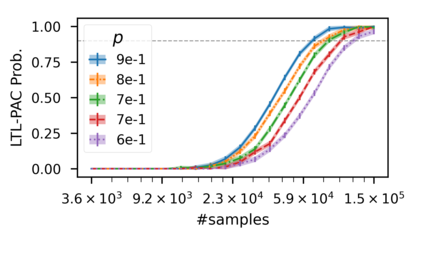
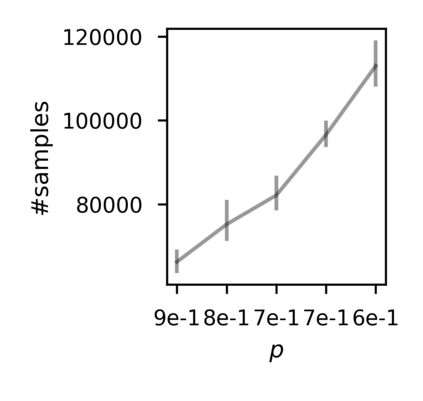
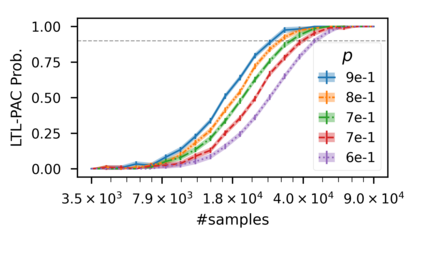
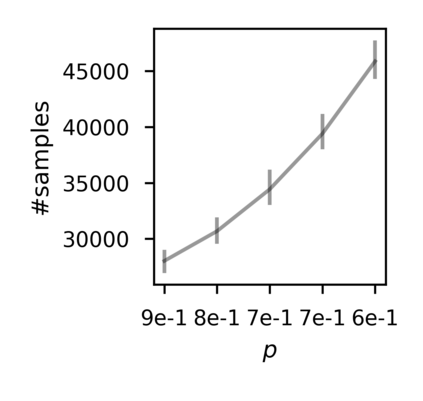
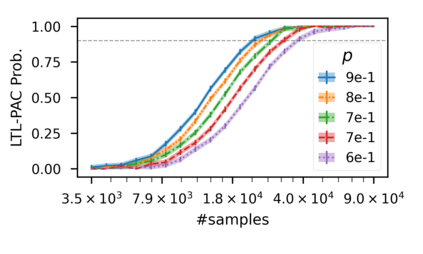
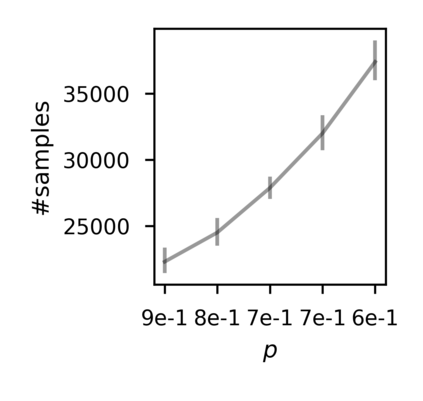
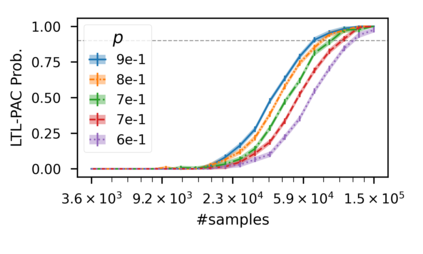
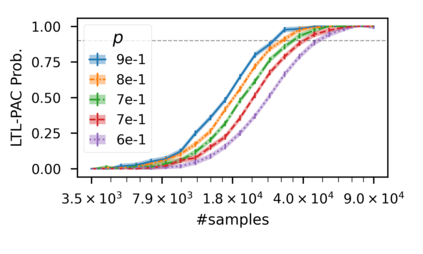
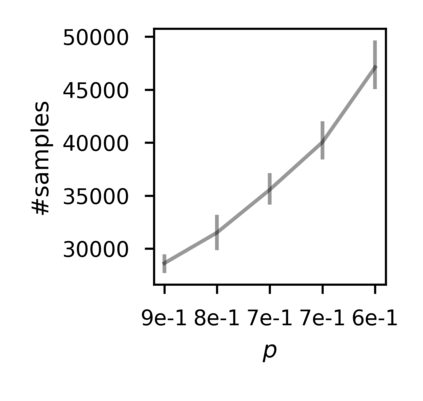
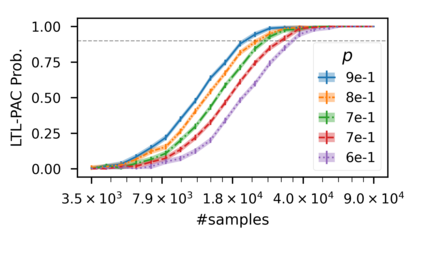
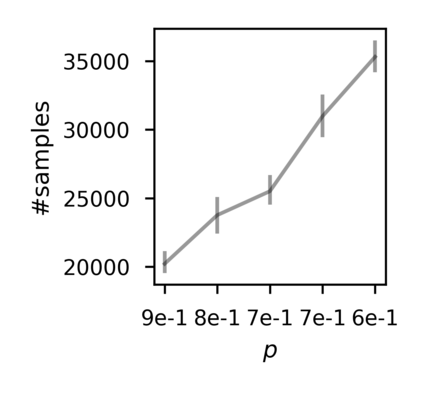
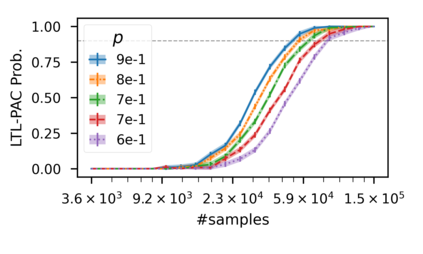
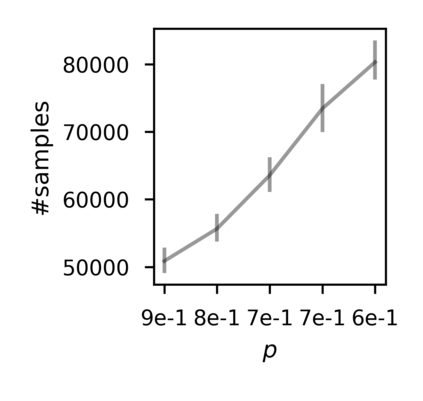
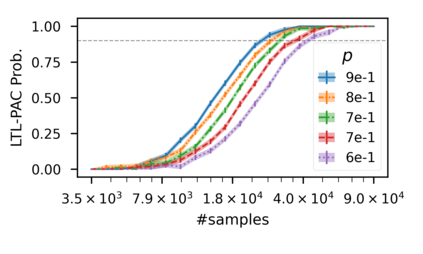
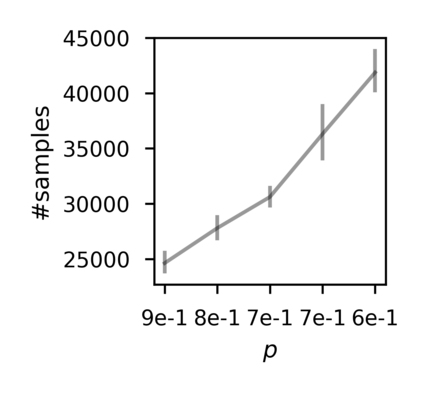
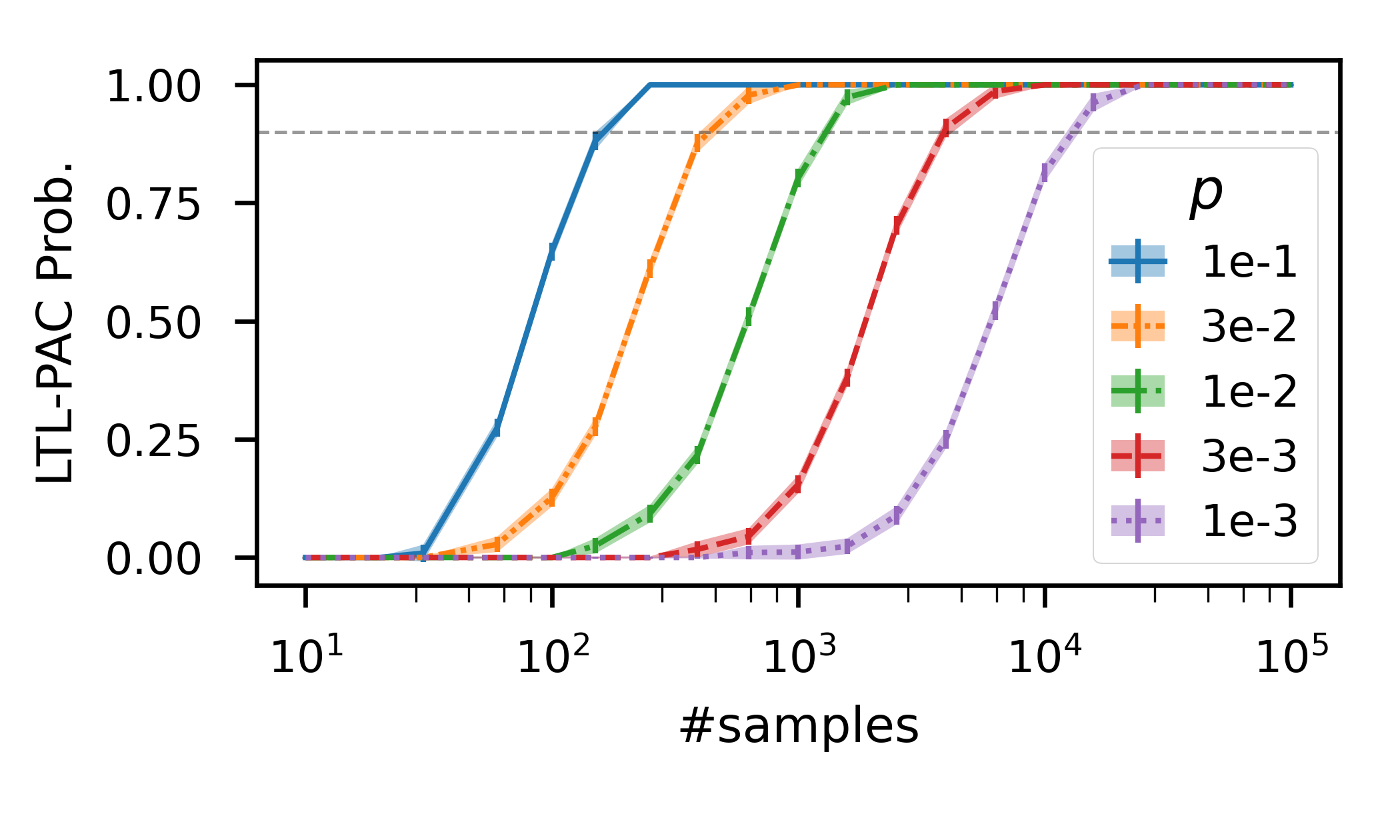
In recent years, researchers have made significant progress in devising reinforcement-learning algorithms for optimizing linear temporal logic (LTL) objectives and LTL-like objectives. Despite these advancements, there are fundamental limitations to how well this problem can be solved that previous studies have alluded to but, to our knowledge, have not examined in depth. In this paper, we address theoretically the hardness of learning with general LTL objectives. We formalize the problem under the probably approximately correct learning in Markov decision processes (PAC-MDP) framework, a standard framework for measuring sample complexity in reinforcement learning. In this formalization, we prove that the optimal policy for any LTL formula is PAC-MDP-learnable only if the formula is in the most limited class in the LTL hierarchy, consisting of only finite-horizon-decidable properties. Practically, our result implies that it is impossible for a reinforcement-learning algorithm to obtain a PAC-MDP guarantee on the performance of its learned policy after finitely many interactions with an unconstrained environment for non-finite-horizon-decidable LTL objectives.
翻译:近年来,研究人员在制定优化线性时间逻辑(LTL)目标和LTL类似目标的强化学习算法方面取得了重大进展。尽管取得了这些进步,但对于以前的研究所暗示但据我们所知没有深入研究的问题,这个问题能在多大程度上得到解决,存在着一些根本性的局限性。在本文件中,我们从理论上处理学习与LTL一般目标的难度问题。我们在Markov决策程序(PAC-MDP)框架(衡量强化学习样本复杂性的标准框架)中将问题正式化。在这个正式化中,我们证明任何LTL公式的最佳政策是PAC-MDP-learn,只有在LTLT等级中公式属于最有限的类别,只有有限-顺差-可减性特性。实际上,我们的结果表明,在与非无限期的LTLT目标的不受限制的环境进行大量互动之后,不可能获得PAC-MDP对其学习政策绩效的保证。