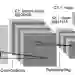
A low-complexity convolutional neural network estimator which learns the minimum mean squared error channel estimator for single-antenna users was recently proposed. We generalize the architecture to the estimation of MIMO channels with multiple-antenna users and incorporate complexity-reducing assumptions based on the channel model. Learning is used in this context to combat the mismatch between the assumptions and real scenarios where the assumptions may not hold. We derive a high-level description of the estimator for arbitrary choices of the pilot sequence. It turns out that the proposed estimator has the implicit structure of a two-layered convolutional neural network, where the derived quantities can be relaxed to learnable parameters. We show that by using discrete Fourier transform based pilots the number of learnable network parameters decreases significantly and the online run time of the estimator is reduced considerably, where we can achieve linearithmic order of complexity in the number of antennas. Numerical results demonstrate performance gains compared to state-of-the-art algorithms from the field of compressive sensing or covariance estimation of the same or even higher computational complexity. The simulation code is available online.
翻译:最近提议了一个低复杂度的神经网络变异网络估计器,用于为单一天文用户学习最小平均值正方差通道估计器。我们将该结构推广到多天文用户对MIMO频道的估计中,并纳入基于频道模型的降低复杂性假设。在此背景下,学习用于消除假设与假设无法维持的真实假设之间的不匹配。我们为任意选择试验序列对估计器的高度描述。结果显示,拟议的估计器具有两层相向神经网络的隐含结构,由此得出的数量可以放松到可学习参数。我们显示,通过使用离散的四维变换实验,可学习网络参数的数量会大幅下降,而估计器的在线运行时间会大大减少,我们可以在天线数中实现线性复杂程度的线性排序。数字结果显示,与从同一或甚至更高的计算复杂性的压缩或同步估计领域得出的最新计算算法相比,业绩会提高。