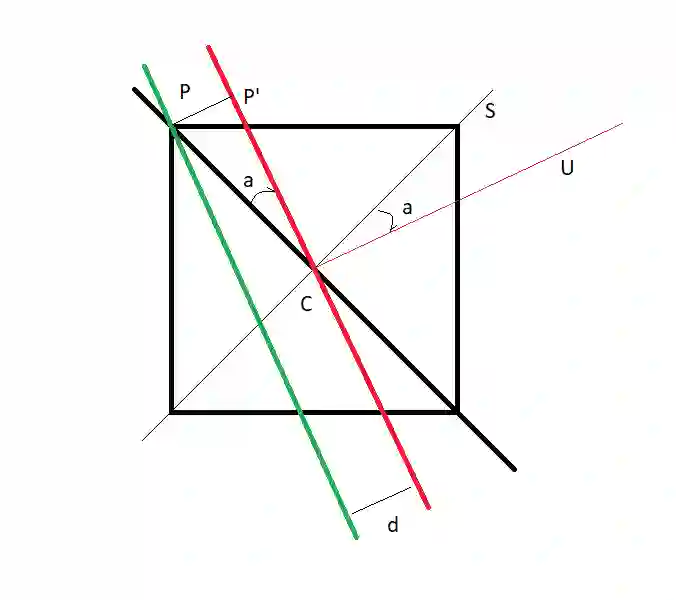
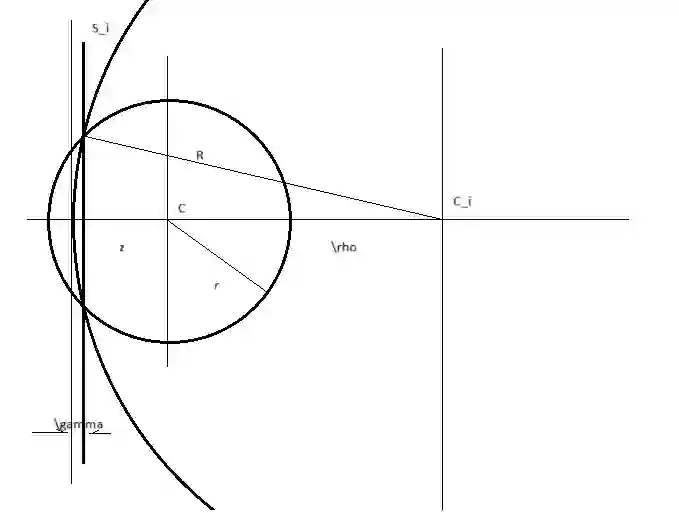
For $S \in \mathbb{N}^n$ and $T \in \mathbb{N}$, the Subset Sum Problem (SSP) $\exists^? x \in \{0,1\}^n $ such that $S^T\cdot x = T$ can be interpreted as the problem of deciding whether the intersection of the positive unit hypercube $Q_n = [0,1]^n$ with the hyperplane $S^T\cdot \left(x - \frac{S}{\|S\|^2 }\cdot T \right) = 0$ contains at least a vertex. In this paper, we give an algorithm of complexity $\mathcal{O}\left( \frac{1}{\epsilon}\cdot n^b \right)$, for some absolute constant $b$, which either proves that there are no vertices in a slab of thickness $\epsilon$ either finds a vertex in the slab of thickness $4\cdot \epsilon$. It is shown that any vertex $P$ in a slab of thickness $\epsilon$ meets $\left| \frac{S^T\cdot P}{T} - 1 \right| \leq \epsilon$, therefore making the proposed algorithm a FPTAS for the SSP. The results are then applied to the study of the so called Simultaneous Subset-Sum Problem (SSSP).
翻译:暂无翻译