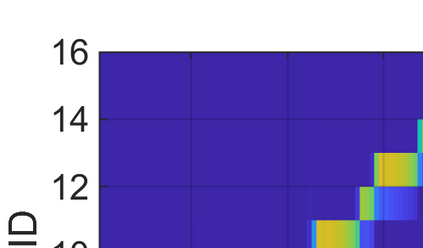
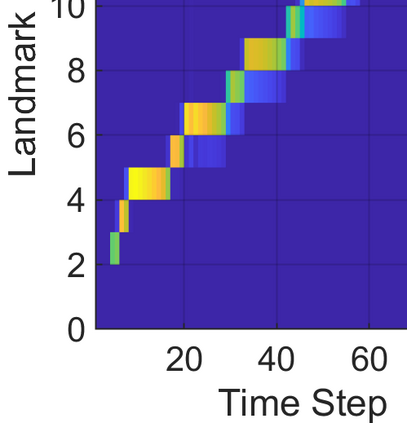
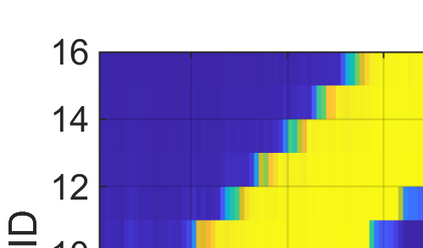
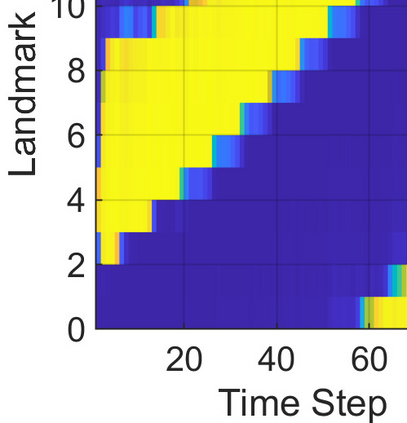
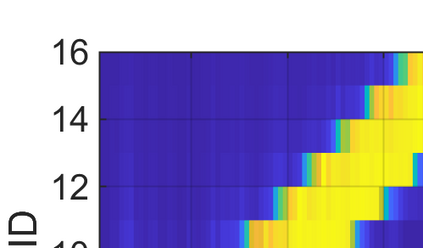
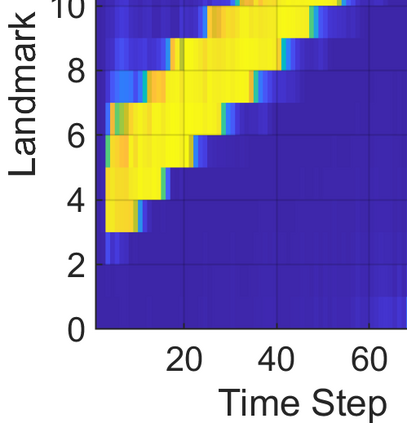
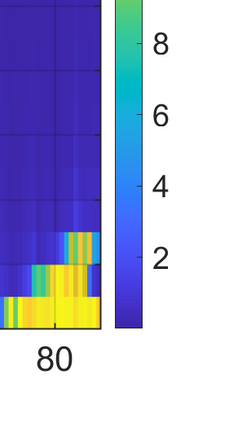
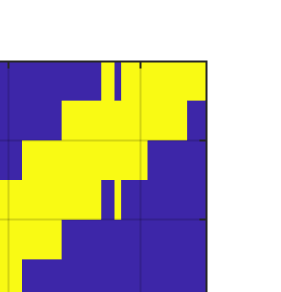
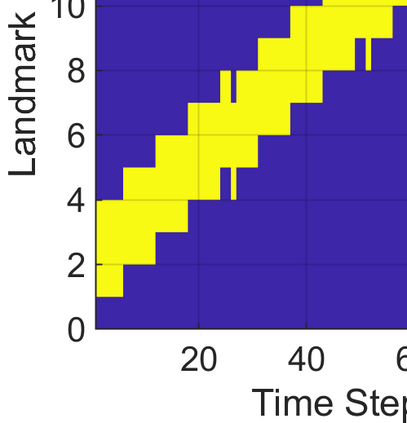
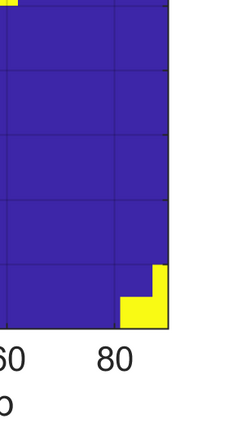
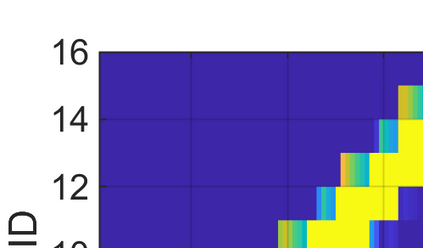
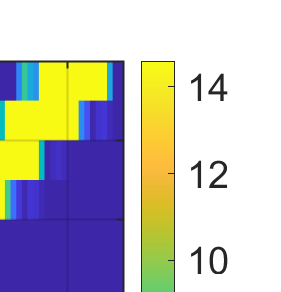
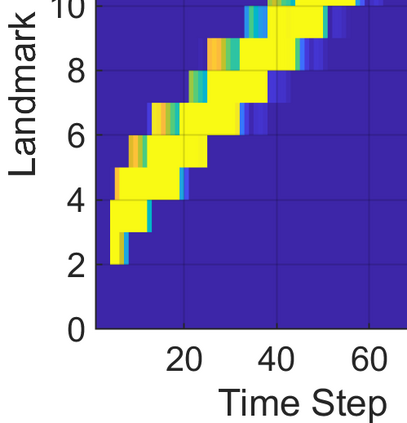
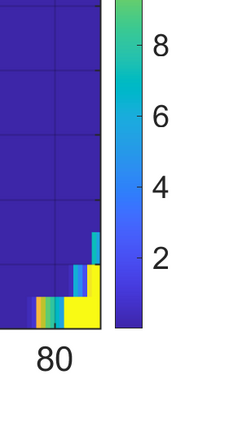
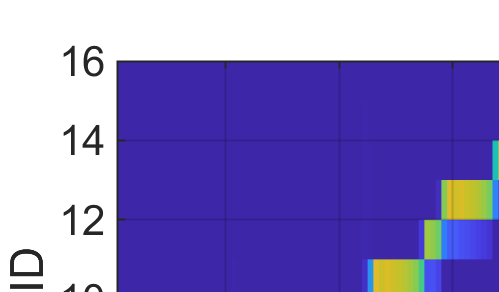
This paper considers the problem of task-dependent (top-down) attention allocation for vision-based autonomous navigation using known landmarks. Unlike the existing paradigm in which landmark selection is formulated as a combinatorial optimization problem, we model it as a resource allocation problem where the decision-maker (DM) is granted extra freedom to control the degree of attention to each landmark. The total resource available to DM is expressed in terms of the capacity limit of the in-take information flow, which is quantified by the directed information from the state of the environment to the DM's observation. We consider a receding horizon implementation of such a controlled sensing scheme in the Linear-Quadratic-Gaussian (LQG) regime. The convex-concave procedure is applied in each time step, whose time complexity is shown to be linear in the horizon length if the alternating direction method of multipliers (ADMM) is used. Numerical studies show that the proposed formulation is sparsity-promoting in the sense that it tends to allocate zero data rate to uninformative landmarks.
翻译:本文件考虑了利用已知的地标对基于愿景的自主导航进行任务依赖(自上而下)的注意力分配问题。与现有的模式不同,在这种模式中,里程碑选择被拟订成组合优化问题,我们把它模拟为一个资源分配问题,在这种模式中,决策者(DM)被给予额外的自由,以控制对每个地标的注意程度。DM可用的总资源用取信息流动的能力限制表示,这种能力限制通过环境状况的定向信息量化到DM的观察中。我们认为,在Linear-Quadratic-Gausian(LQG)制度中,这种受控的遥感计划的实施将重新放弃地平线。Convex-concaveve(LQG)程序在每一步骤中都适用,如果使用交替的乘数法(ADMM),其时间复杂性在地平线长度上显示为线性。数字研究显示,拟议的提法是松动的,因为它倾向于将零数据率分配给非说明性的标志。