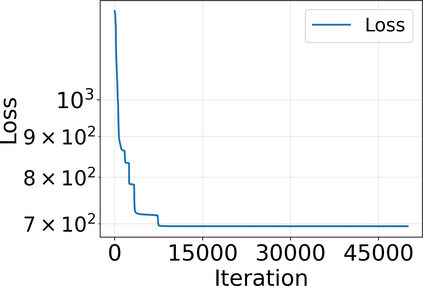
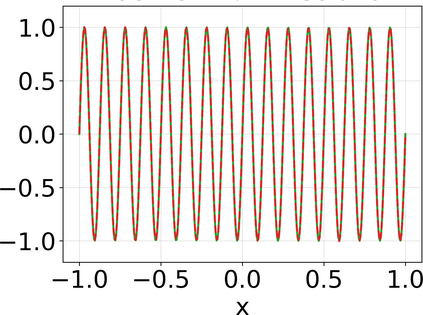
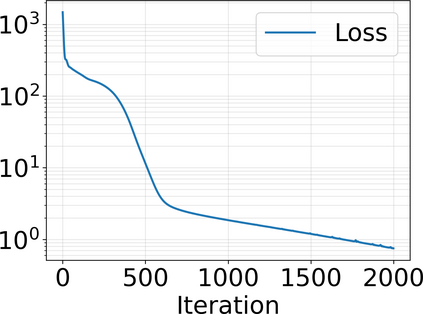
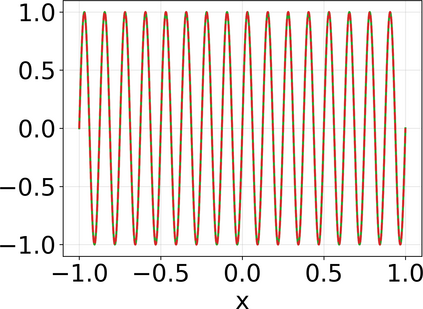
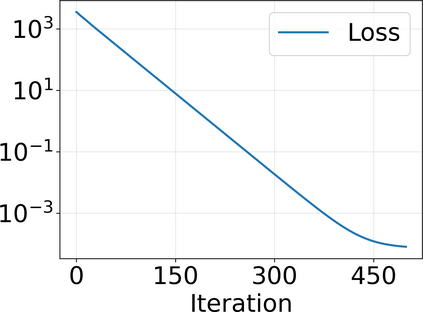
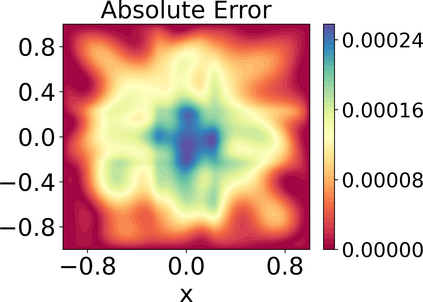
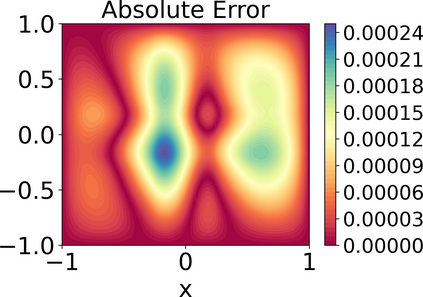
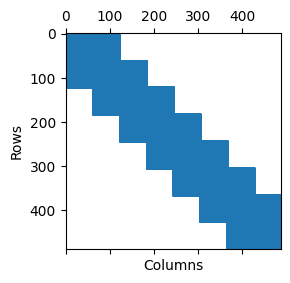
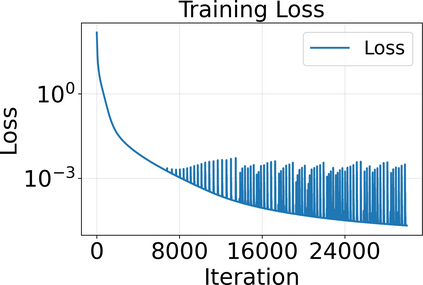
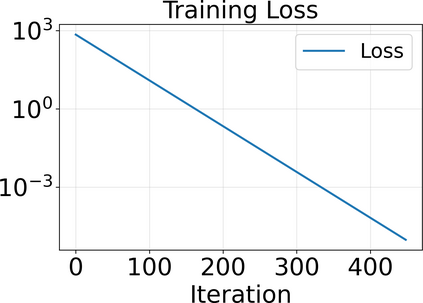
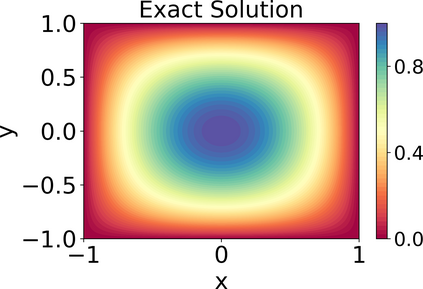
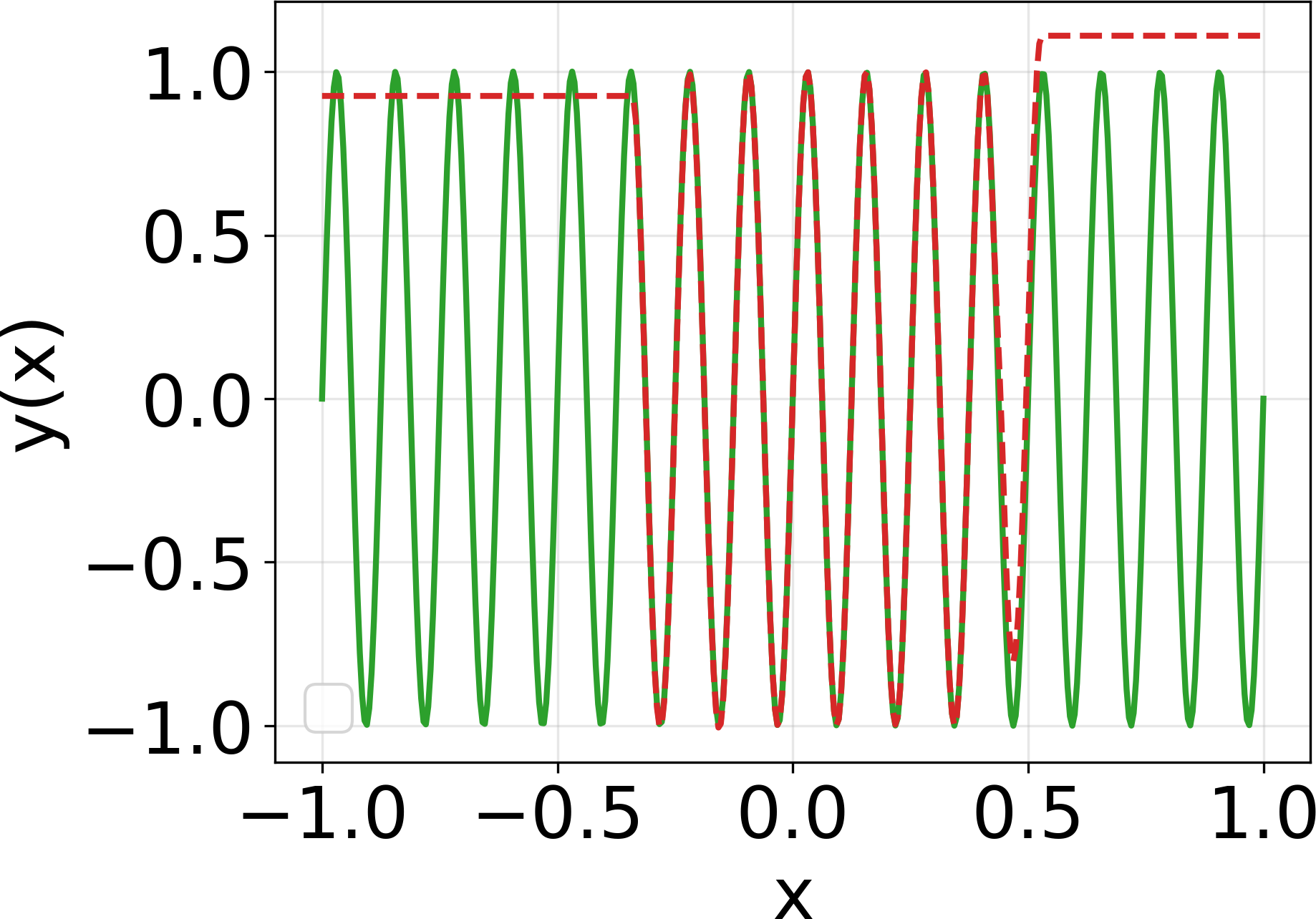
Approximating the solutions of boundary value problems governed by partial differential equations with neural networks is challenging, largely due to the difficult training process. This difficulty can be partly explained by the spectral bias, that is, the slower convergence of high-frequency components, and can be mitigated by localizing neural networks via (overlapping) domain decomposition. We combine this localization with the Gauss-Newton method as the optimizer to obtain faster convergence than gradient-based schemes such as Adam; this comes at the cost of solving an ill-conditioned linear system in each iteration. Domain decomposition induces a block-sparse structure in the otherwise dense Gauss-Newton system, reducing the computational cost per iteration. Our numerical results indicate that combining localization and Gauss-Newton optimization is promising for neural network-based solvers for partial differential equations.
翻译:暂无翻译