Momentum Centering and Asynchronous Update for Adaptive Gradient Methods

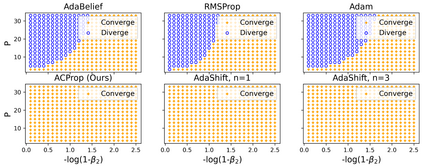
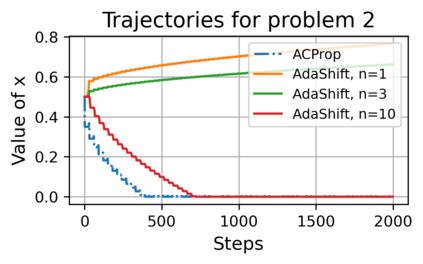
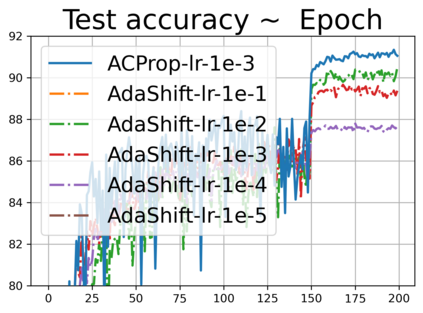
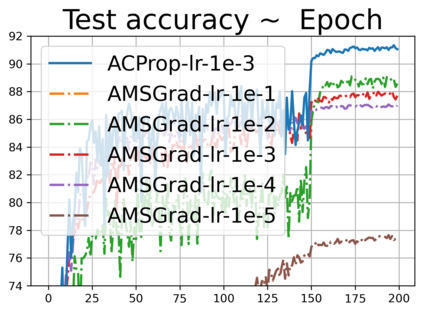
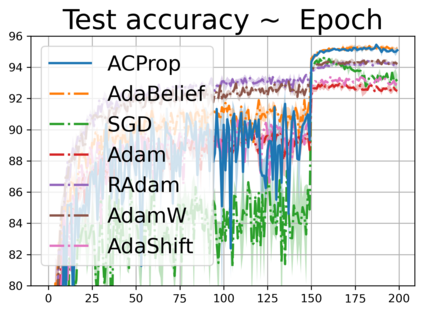
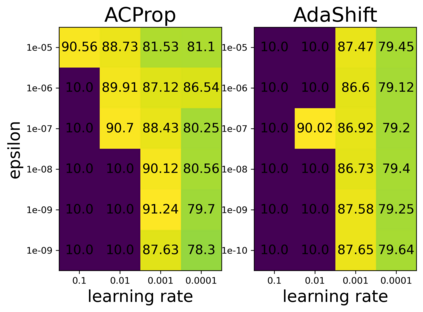
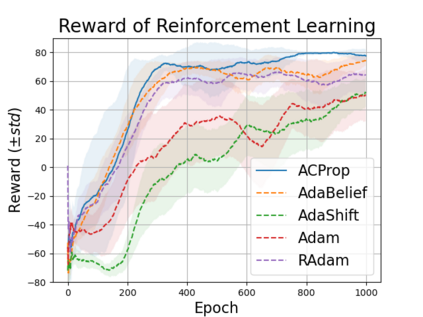
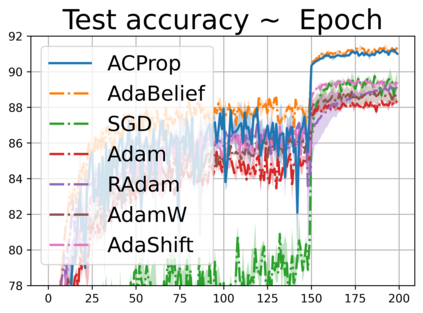
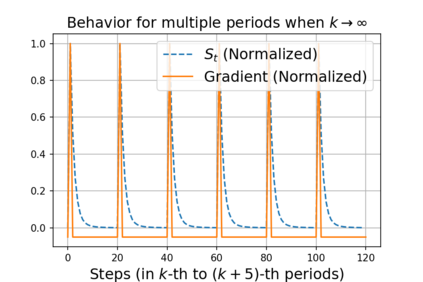
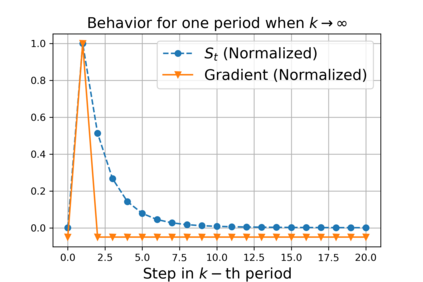
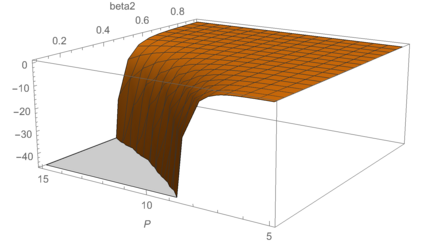
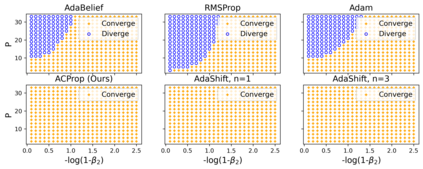
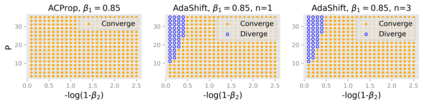
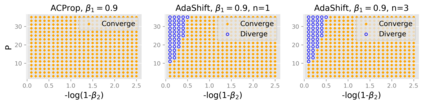
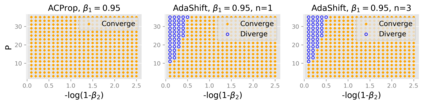
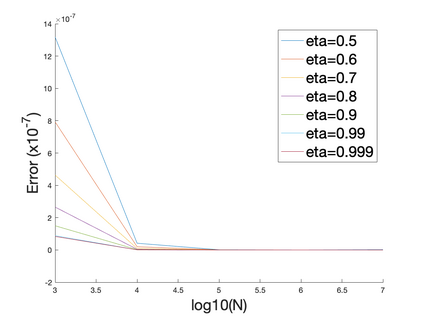
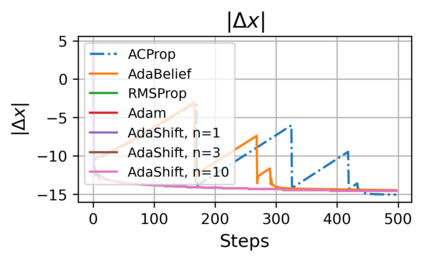
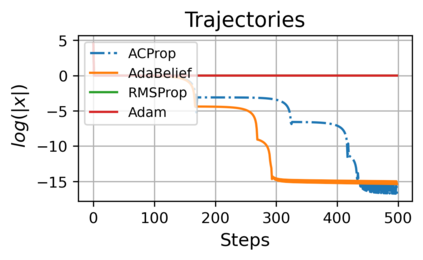
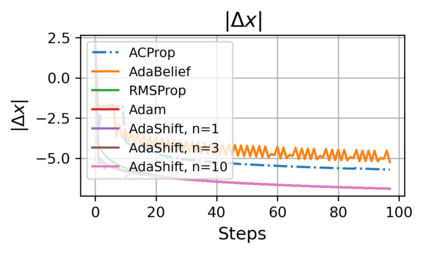
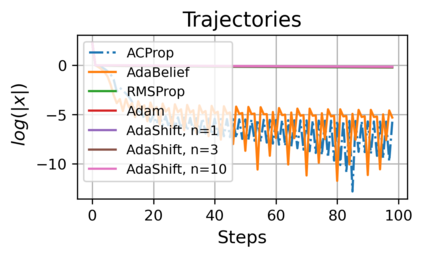
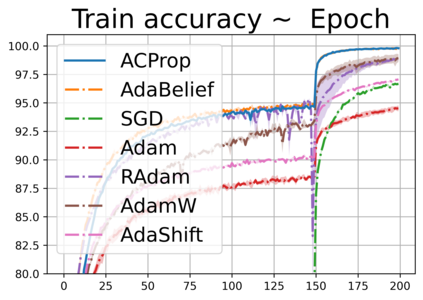
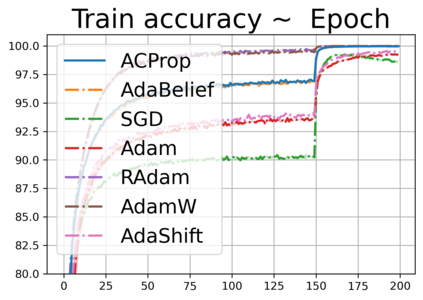
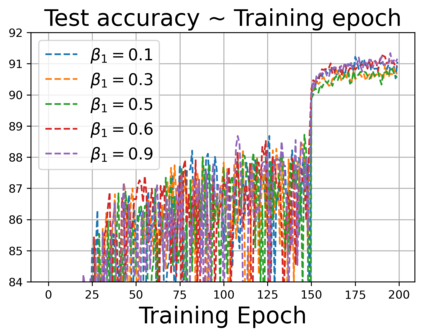
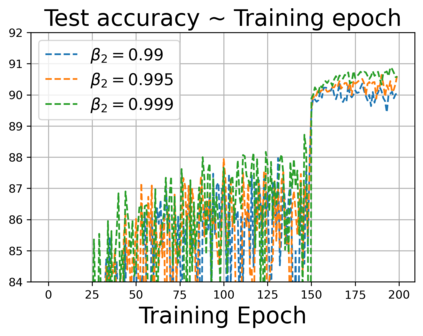
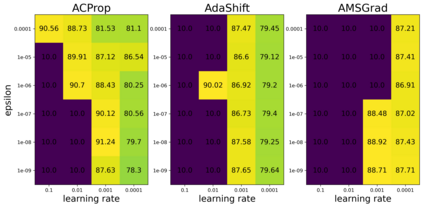
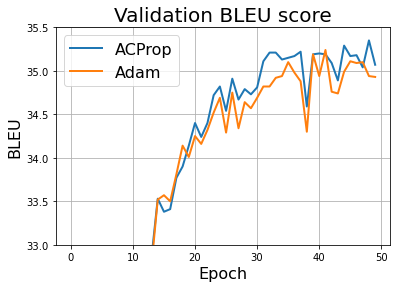
We propose ACProp (Asynchronous-centering-Prop), an adaptive optimizer which combines centering of second momentum and asynchronous update (e.g. for $t$-th update, denominator uses information up to step $t-1$, while numerator uses gradient at $t$-th step). ACProp has both strong theoretical properties and empirical performance. With the example by Reddi et al. (2018), we show that asynchronous optimizers (e.g. AdaShift, ACProp) have weaker convergence condition than synchronous optimizers (e.g. Adam, RMSProp, AdaBelief); within asynchronous optimizers, we show that centering of second momentum further weakens the convergence condition. We demonstrate that ACProp has a convergence rate of $O(\frac{1}{\sqrt{T}})$ for the stochastic non-convex case, which matches the oracle rate and outperforms the $O(\frac{logT}{\sqrt{T}})$ rate of RMSProp and Adam. We validate ACProp in extensive empirical studies: ACProp outperforms both SGD and other adaptive optimizers in image classification with CNN, and outperforms well-tuned adaptive optimizers in the training of various GAN models, reinforcement learning and transformers. To sum up, ACProp has good theoretical properties including weak convergence condition and optimal convergence rate, and strong empirical performance including good generalization like SGD and training stability like Adam.