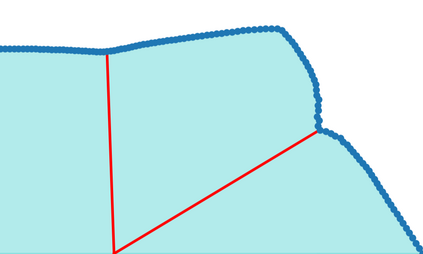
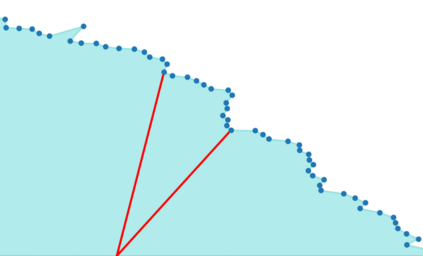
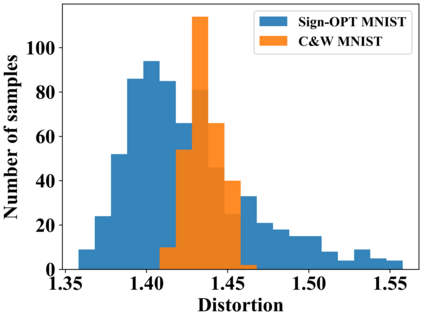
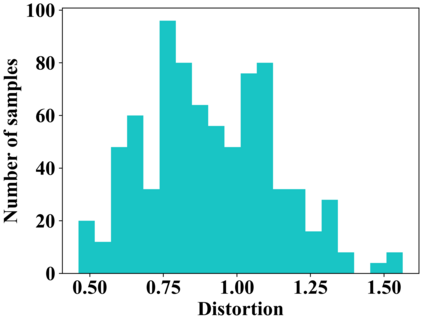
Adversarial example generation becomes a viable method for evaluating the robustness of a machine learning model. In this paper, we consider hard-label black-box attacks (a.k.a. decision-based attacks), which is a challenging setting that generates adversarial examples based on only a series of black-box hard-label queries. This type of attacks can be used to attack discrete and complex models, such as Gradient Boosting Decision Tree (GBDT) and detection-based defense models. Existing decision-based attacks based on iterative local updates often get stuck in a local minimum and fail to generate the optimal adversarial example with the smallest distortion. To remedy this issue, we propose an efficient meta algorithm called BOSH-attack, which tremendously improves existing algorithms through Bayesian Optimization (BO) and Successive Halving (SH). In particular, instead of traversing a single solution path when searching an adversarial example, we maintain a pool of solution paths to explore important regions. We show empirically that the proposed algorithm converges to a better solution than existing approaches, while the query count is smaller than applying multiple random initializations by a factor of 10.
翻译:Aversarial 样板生成成为评估机器学习模型的稳健性的一种可行方法。 在本文中, 我们考虑硬标签黑盒攻击( a.k.a.a. 以决定为基础的攻击) 。 硬标签黑盒攻击( a.k.a. ) 是一个具有挑战性的环境, 仅基于一系列黑盒硬标签查询, 产生对抗性的例子。 这种攻击可以用来攻击离散和复杂的模型, 如“ 梯度推动决定树” 和基于探测的防御模型。 以迭代本地更新为基础的现有基于决定的攻击往往被困在本地最小的最小范围内, 无法生成最优的对抗性例子 。 为了纠正这个问题, 我们提议了一个称为 BOSH 攻击的高效元算法, 它通过Bayesian Optimination (OBO) 和 Conthive Halvive (SH) 大大改进了现有的算法。 。 特别是, 在搜索一个对抗性范例时, 我们保留了一个解决方案路径库以探索重要区域。 我们从经验上表明, 提议的算算算算算算算算算算算法会比现有方法更好的解决办法, 。 而小于用一个10 系数的多重随机初始化系数比应用一个系数小于多个。