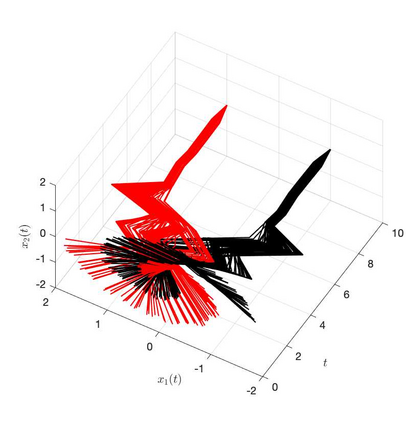
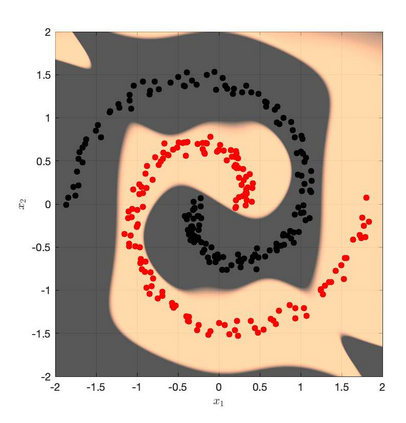
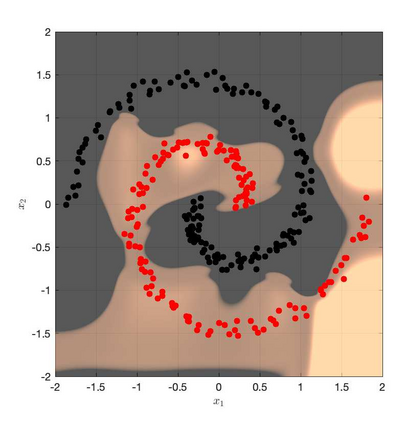
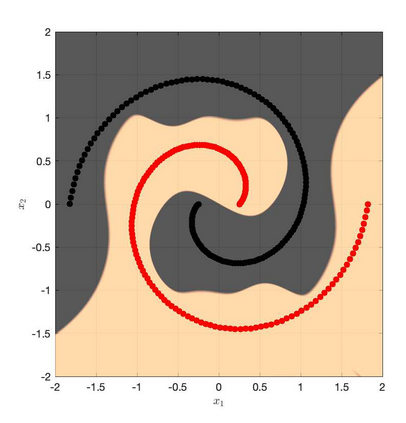
It is well-known that the training of Deep Neural Networks (DNN) can be formalized in the language of optimal control. In this context, this paper leverages classical turnpike properties of optimal control problems to attempt a quantifiable answer to the question of how many layers should be considered in a DNN. The underlying assumption is that the number of neurons per layer -- i.e., the width of the DNN -- is kept constant. Pursuing a different route than the classical analysis of approximation properties of sigmoidal functions, we prove explicit bounds on the required depths of DNNs based on asymptotic reachability assumptions and a dissipativity-inducing choice of the regularization terms in the training problem. Numerical results obtained for the two spiral task data set for classification indicate that the proposed estimates can provide non-conservative depth bounds.
翻译:众所周知,深海神经网络(DNN)的培训可以用最佳控制语言正式确定,在这方面,本文件利用了最佳控制问题古老的转弯特性,试图用量化的方法回答DNN中应考虑多少层的问题。 基本假设是,每层神经元的数量 -- -- 即DNN的宽度 -- -- 保持不变。我们采用不同于典型的对Sigmodil函数近似特性分析的路线,我们证明,根据无药可及性可达性假设和对培训问题中正规化条件的选择,对DNN的要求深度有明确的界限。两个螺旋任务分类数据集获得的数字结果表明,拟议的估计数可以提供非保守的深度界限。