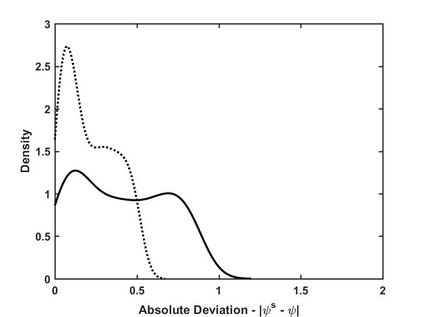
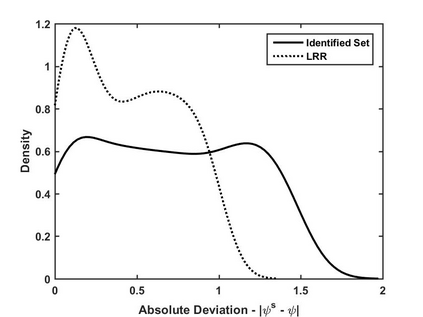
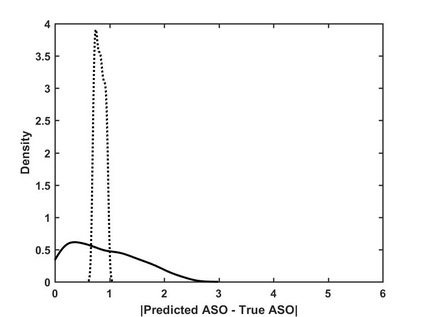
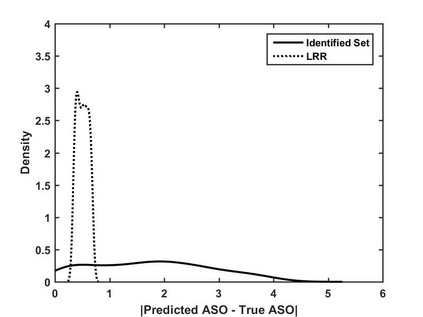
Structural models that admit multiple reduced forms, such as game-theoretic models with multiple equilibria, pose challenges in practice, especially when parameters are set-identified and the identified set is large. In such cases, researchers often choose to focus on a particular subset of equilibria for counterfactual analysis, but this choice can be hard to justify. This paper shows that some parameter values can be more "desirable" than others for counterfactual analysis, even if they are empirically equivalent given the data. In particular, within the identified set, some counterfactual predictions can exhibit more robustness than others, against local perturbations of the reduced forms (e.g. the equilibrium selection rule). We provide a representation of this subset which can be used to simplify the implementation. We illustrate our message using moment inequality models, and provide an empirical application based on a model with top-coded data.
翻译:接受多种简化形式的结构模型,如具有多重平衡的游戏理论模型等,在实践上构成挑战,特别是当参数被确定,而且所查明的数据集很大时。在这种情况下,研究人员往往选择侧重于一个特定的平衡子子群,用于反事实分析,但这一选择可能难以证明。本文表明,某些参数值比其他参数值更“可取”,用于反事实分析,即使根据数据,这些参数值在经验上与数据相当。特别是,在所查明的一组中,一些反事实预测比其他预测显示得更稳健,而减少的形态的局部扰动(例如均衡选择规则)则比其他预测更强。我们提供了这一子群子群的描述,可用于简化执行过程。我们用瞬间不平等模型来说明我们的信息,并提供基于顶级编码数据模型的经验应用。