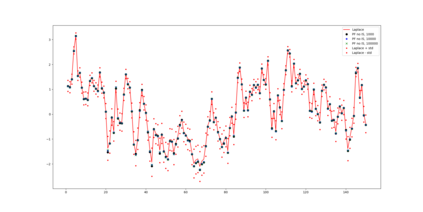
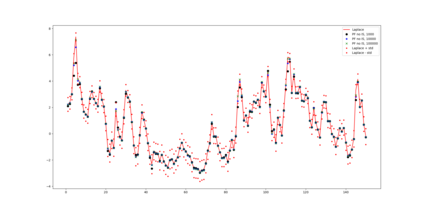
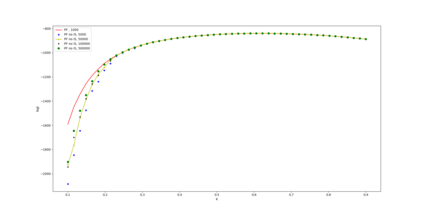
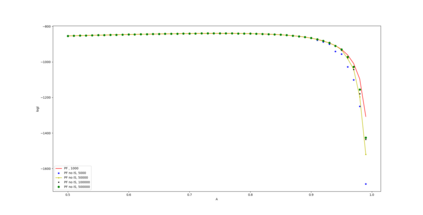
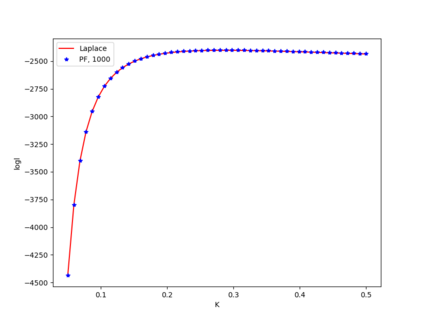
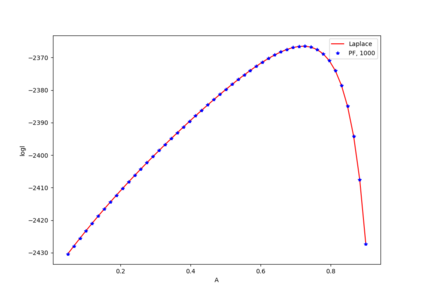
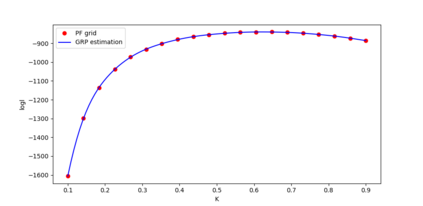
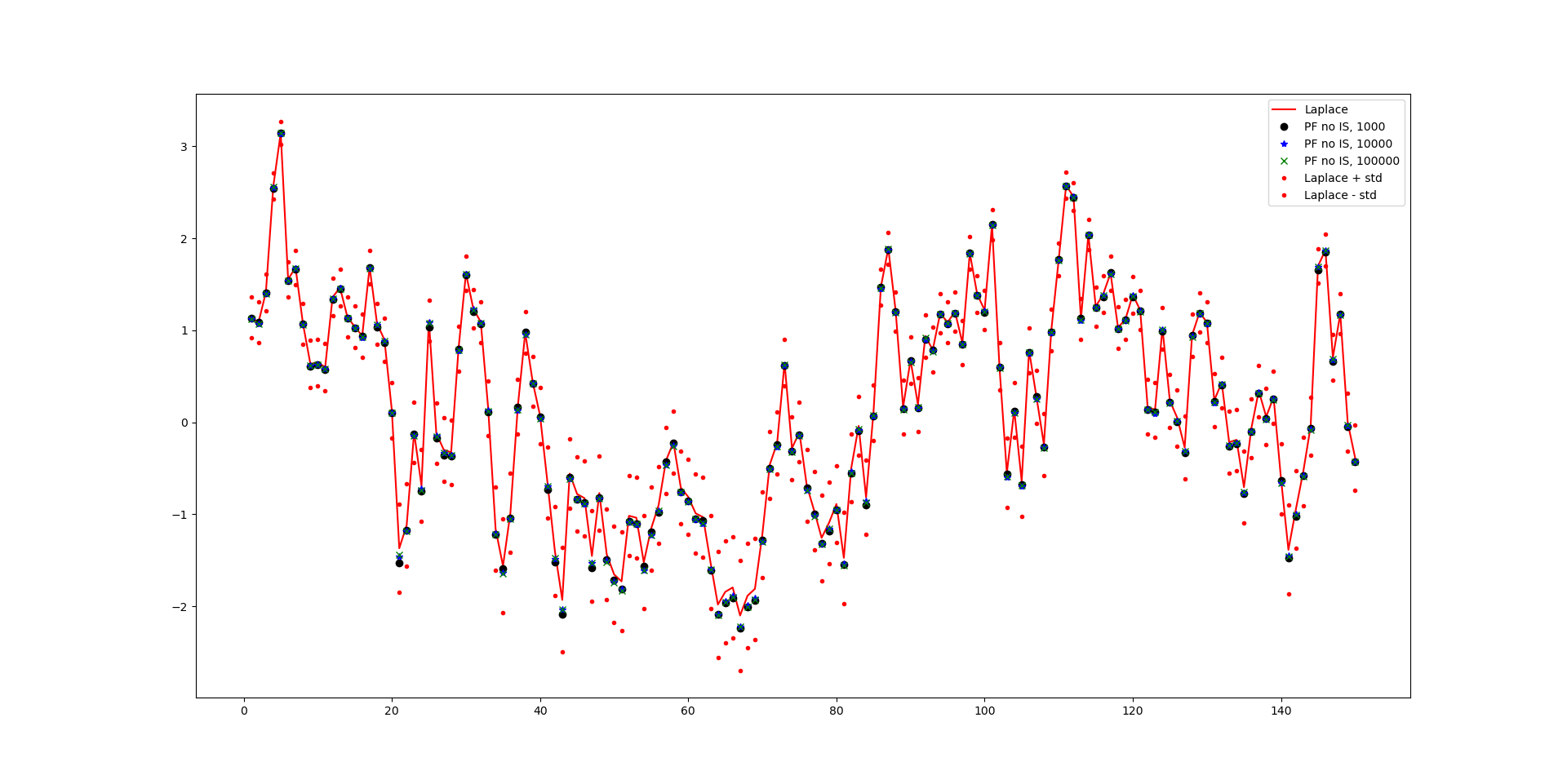
In this paper we develop Maximum likelihood (ML) based algorithms to calibrate the model parameters in credit rating transition models. Since the credit rating transition models are not Gaussian linear models, the celebrated Kalman filter is not suitable to compute the likelihood of observed migrations. Therefore, we develop a Laplace approximation of the likelihood function and as a result the Kalman filter can be used in the end to compute the likelihood function. This approach is applied to so-called high-default portfolios, in which the number of migrations (defaults) is large enough to obtain high accuracy of the Laplace approximation. By contrast, low-default portfolios have a limited number of observed migrations (defaults). Therefore, in order to calibrate low-default portfolios, we develop a ML algorithm using a particle filter (PF) and Gaussian process regression. Experiments show that both algorithms are efficient and produce accurate approximations of the likelihood function and the ML estimates of the model parameters.
翻译:暂无翻译