Parallel Private Retrieval of Merkle Proofs via Tree Colorings

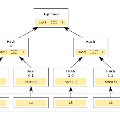
Motivated by a practical scenario in blockchains in which a client, who possesses a transaction, wishes to privately verify that the transaction actually belongs to a block, we investigate the problem of private retrieval of Merkle proofs (i.e. proofs of inclusion/membership) in a Merkle tree. In this setting, one or more servers store the nodes of a binary tree (a Merkle tree), while a client wants to retrieve the set of nodes along a root-to-leaf path (i.e. a Merkle proof, after appropriate node swapping operations), without letting the servers know which path is being retrieved. We propose a method that partitions the Merkle tree to enable parallel private retrieval of the Merkle proofs. The partitioning step is based on a novel tree coloring called ancestral coloring in which nodes with ancestor-descendant relationship must have distinct colors. To minimize the retrieval time, the coloring must be balanced, i.e. the sizes of the color classes must differ by at most one. We develop a fast algorithm to find a balanced ancestral coloring in almost linear time in the number of tree nodes, which can handle trees with billions of nodes in minutes. Unlike existing approaches, ours allows an efficient indexing with polylog time and space complexity. Our partitioning method can be applied on top of any private information retrieval scheme, leading to the minimum storage overhead and fastest running time compared to existing works.