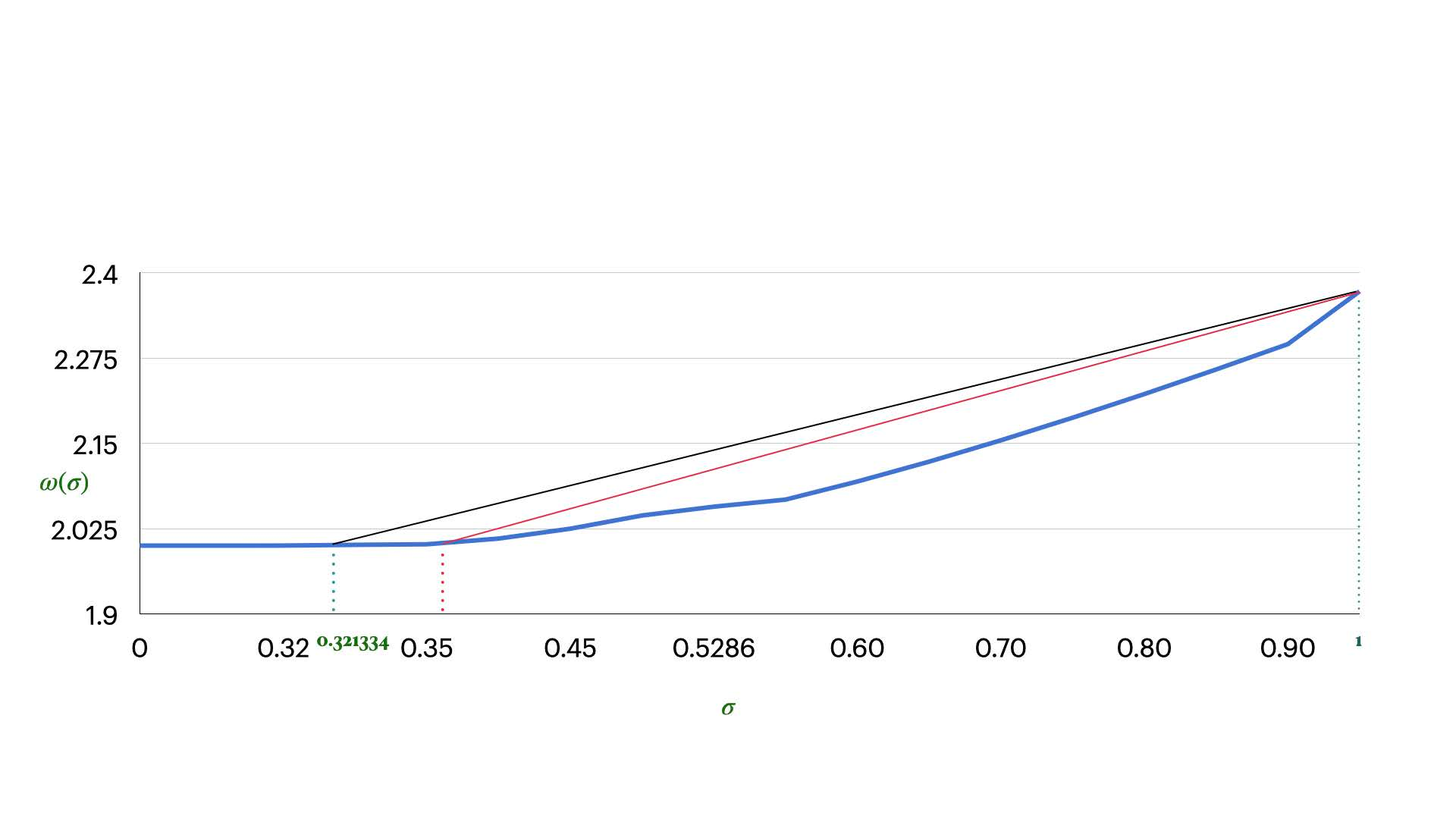
Given an $n$-vertex $m$-edge digraph $G = (V,E)$ and a set $S \subseteq V$, $|S| = n^{\sigma}$ (for some $0 < \sigma \le 1$) of designated sources, the $S \times V$-direachability problem is to compute for every $s \in S$, the set of all the vertices reachable from $s$ in $G$. Known naive algorithms for this problem either run a BFS/DFS separately from every source, and as a result require $O(m \cdot n^{\sigma})$ time, or compute the transitive closure of $G$ in $\tilde O(n^{\omega})$ time, where $\omega < 2.371552\ldots$ is the matrix multiplication exponent. Hence, the current state-of-the-art bound for the problem on graphs with $m = \Theta(n^{\mu})$ edges in $\tilde O(n^{\min \{\mu + \sigma, \omega \}})$. Our first contribution is an algorithm with running time $\tilde O(n^{1 + \tiny{\frac{2}{3}} \omega(\sigma)})$ for this problem, where $\omega(\sigma)$ is the rectangular matrix multiplication exponent. Using current state-of-the-art estimates on $\omega(\sigma)$, our exponent is better than $\min \{2 + \sigma, \omega \}$ for $\tilde \sigma \le \sigma \le 0.53$, where $1/3 < \tilde \sigma < 0.3336$ is a universal constant. Our second contribution is a sequence of algorithms $\mathcal A_0, \mathcal A_1, \mathcal A_2, \ldots$ for the $S \times V$-direachability problem. We argue that under a certain assumption that we introduce, for every $\tilde \sigma \le \sigma < 1$, there exists a sufficiently large index $k = k(\sigma)$ so that $\mathcal A_k$ improves upon the current state-of-the-art bounds for $S \times V$-direachability with $|S| = n^{\sigma}$, in the densest regime $\mu =2$. We show that to prove this assumption, it is sufficient to devise an algorithm that computes a rectangular max-min matrix product roughly as efficiently as ordinary $(+, \cdot)$ matrix product. Our algorithms heavily exploit recent constructions of directed shortcuts by Kogan and Parter.
翻译:暂无翻译