Quantifying the Unknown: Impact of Segmentation Uncertainty on Image-Based Simulations

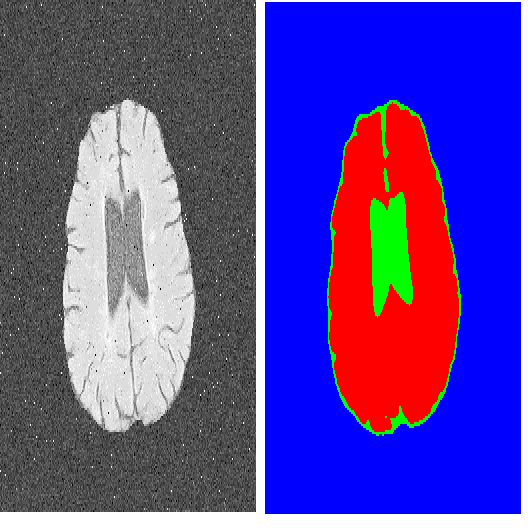
Image-based simulation, the use of 3D images to calculate physical quantities, fundamentally relies on image segmentation to create the computational geometry. However, this process introduces image segmentation uncertainty because there is a variety of different segmentation tools (both manual and machine-learning-based) that will each produce a unique and valid segmentation. First, we demonstrate that these variations propagate into the physics simulations, compromising the resulting physics quantities. Second, we propose a general framework for rapidly quantifying segmentation uncertainty. Through the creation and sampling of segmentation uncertainty probability maps, we systematically and objectively create uncertainty distributions of the physics quantities. We show that physics quantity uncertainty distributions can follow a Normal distribution, but, in more complicated physics simulations, the resulting uncertainty distribution can be both nonintuitive and surprisingly nontrivial. We also establish that simply bounding the uncertainty can fail in situations that are sensitive to image segmentation. While our work does not eliminate segmentation uncertainty, it makes visible the previously unrecognized range of uncertainty currently plaguing image-based simulation, enabling more credible simulations.