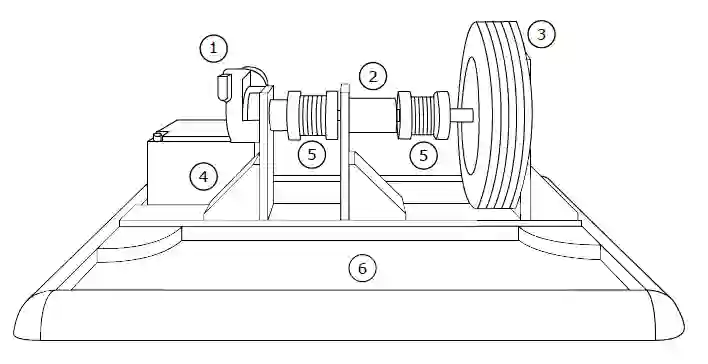
Inferring parameter distributions of complex industrial systems from noisy time series data requires methods to deal with the uncertainty of the underlying data and the used simulation model. Bayesian inference is well suited for these uncertain inverse problems. Standard methods used to identify uncertain parameters are Markov Chain Monte Carlo (MCMC) methods with explicit evaluation of a likelihood function. However, if the likelihood is very complex, such that its evaluation is computationally expensive, or even unknown in its explicit form, Approximate Bayesian Computation (ABC) methods provide a promising alternative. In this work both methods are first applied to artificially generated data and second on a real world problem, by using data of an electric motor test bench. We show that both methods are able to infer the distribution of varying parameters with a Bayesian hierarchical approach. But the proposed ABC method is computationally much more efficient in order to achieve results with similar accuracy. We suggest to use summary statistics in order to reduce the dimension of the data which significantly increases the efficiency of the algorithm. Further the simulation model is replaced by a Polynomial Chaos Expansion (PCE) surrogate to speed up model evaluations. We proof consistency for the proposed surrogate-based ABC method with summary statistics under mild conditions on the (approximated) forward model.
翻译:从噪音的时间序列数据推断复杂工业系统参数分布的方法来自噪音的时间序列数据,要求用各种方法处理基础数据和所用模拟模型的不确定性。贝叶斯推断非常适合这些不确定的反向问题。用于确定不确定参数的标准方法是Markov 链锁蒙特卡洛(MC MC) 方法,对可能性功能进行明确的评价。但是,如果可能性非常复杂,其评估费用昂贵,甚至以其明确的形式为形式而未知,则其评估方法提供了一种有希望的替代办法。在这项工作中,两种方法首先应用于人为生成的数据,其次于真实的世界问题,方法是使用电动发动机测试台的数据。我们表明,两种方法都能够用巴伊斯等级方法推断不同参数的分布情况。但是,拟议的ABC方法在计算上效率要高得多,以便以类似准确的方式取得结果。我们建议使用摘要统计数据,以便减少大大提高算法效率的数据的维度。进一步用模拟模型取代模拟模型取代人工生成的数据,然后使用电动发动机试验台的数据,用电动发动机试验台的数据来推断不同参数的分布情况。我们在模型下,我们用BCM-BC模型下,用BS-C-C-Gregirgirglate的模型,以模拟数据进行一致。我们用A-C-C-C-C-C-C-Sirgregalgalevalevalvilgilgy 证据证明。