Bandwidth-Optimal Random Shuffling for GPUs

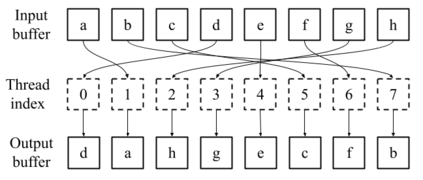
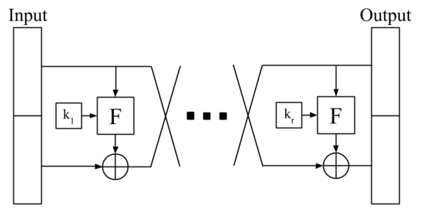
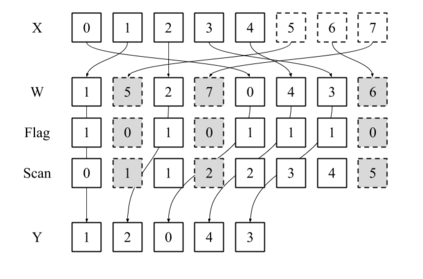
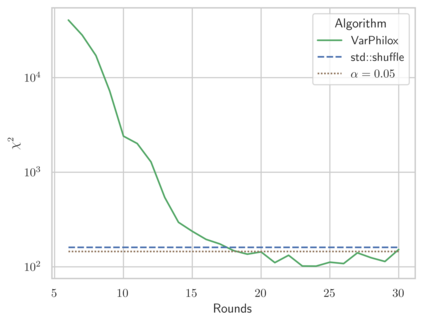
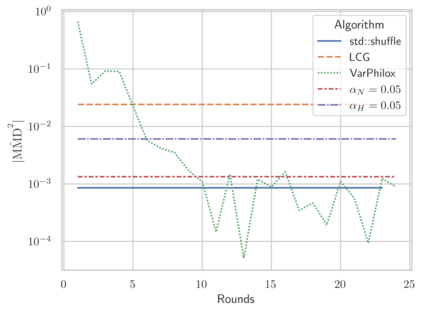
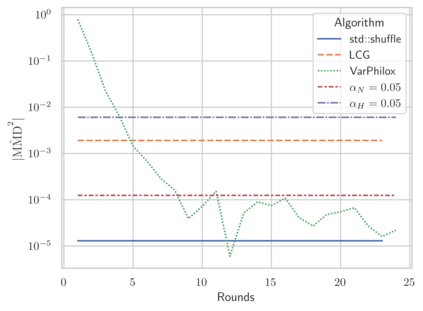
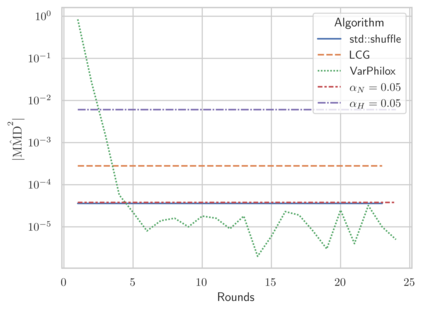
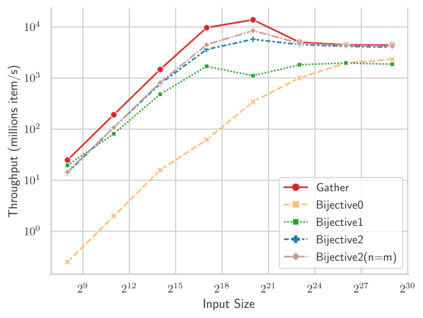
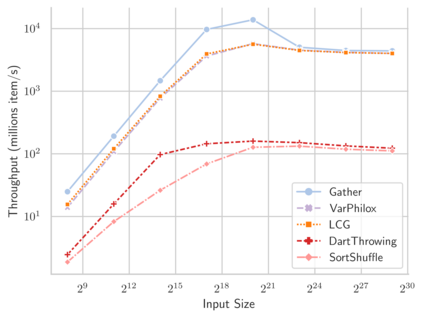
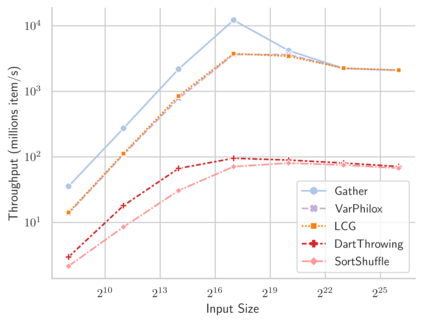
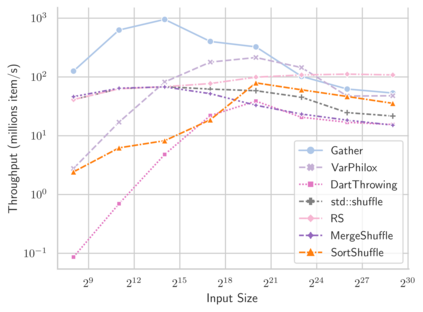
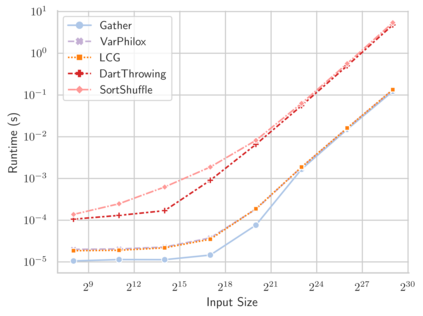
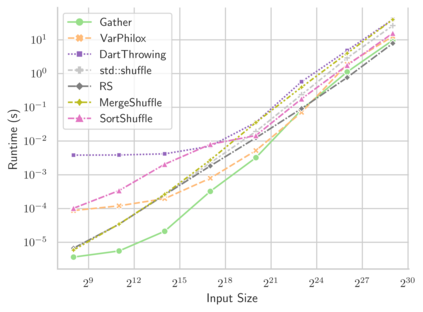
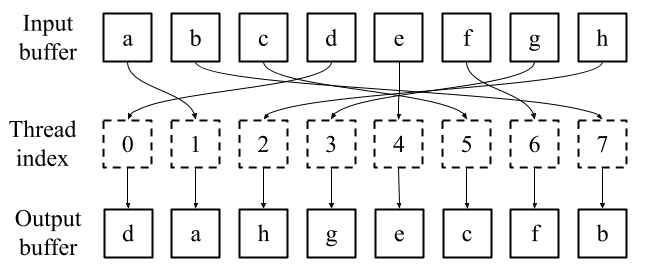
Linear-time algorithms that are traditionally used to shuffle data on CPUs, such as the method of Fisher-Yates, are not well suited to implementation on GPUs due to inherent sequential dependencies, and existing parallel shuffling algorithms are unsuitable for GPU architectures because they incur a large number of read/write operations to high latency global memory. To address this, we provide a method of generating pseudo-random permutations in parallel by fusing suitable pseudo-random bijective functions with stream compaction operations. Our algorithm, termed `bijective shuffle' trades increased per-thread arithmetic operations for reduced global memory transactions. It is work-efficient, deterministic, and only requires a single global memory read and write per shuffle input, thus maximising use of global memory bandwidth. To empirically demonstrate the correctness of the algorithm, we develop a statistical test for the quality of pseudo-random permutations based on kernel space embeddings. Experimental results show that the bijective shuffle algorithm outperforms competing algorithms on GPUs, showing improvements of between one and two orders of magnitude and approaching peak device bandwidth.