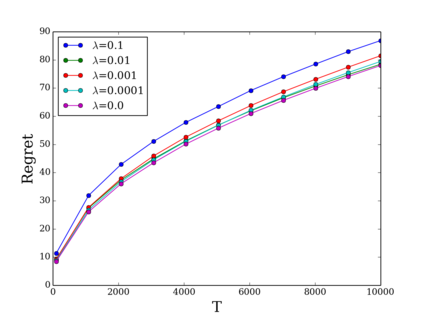
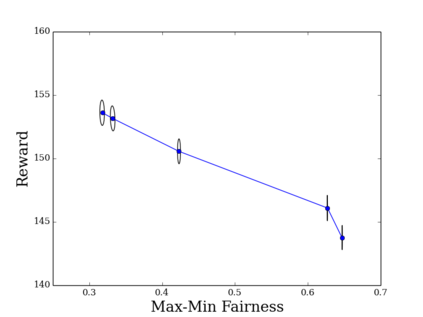
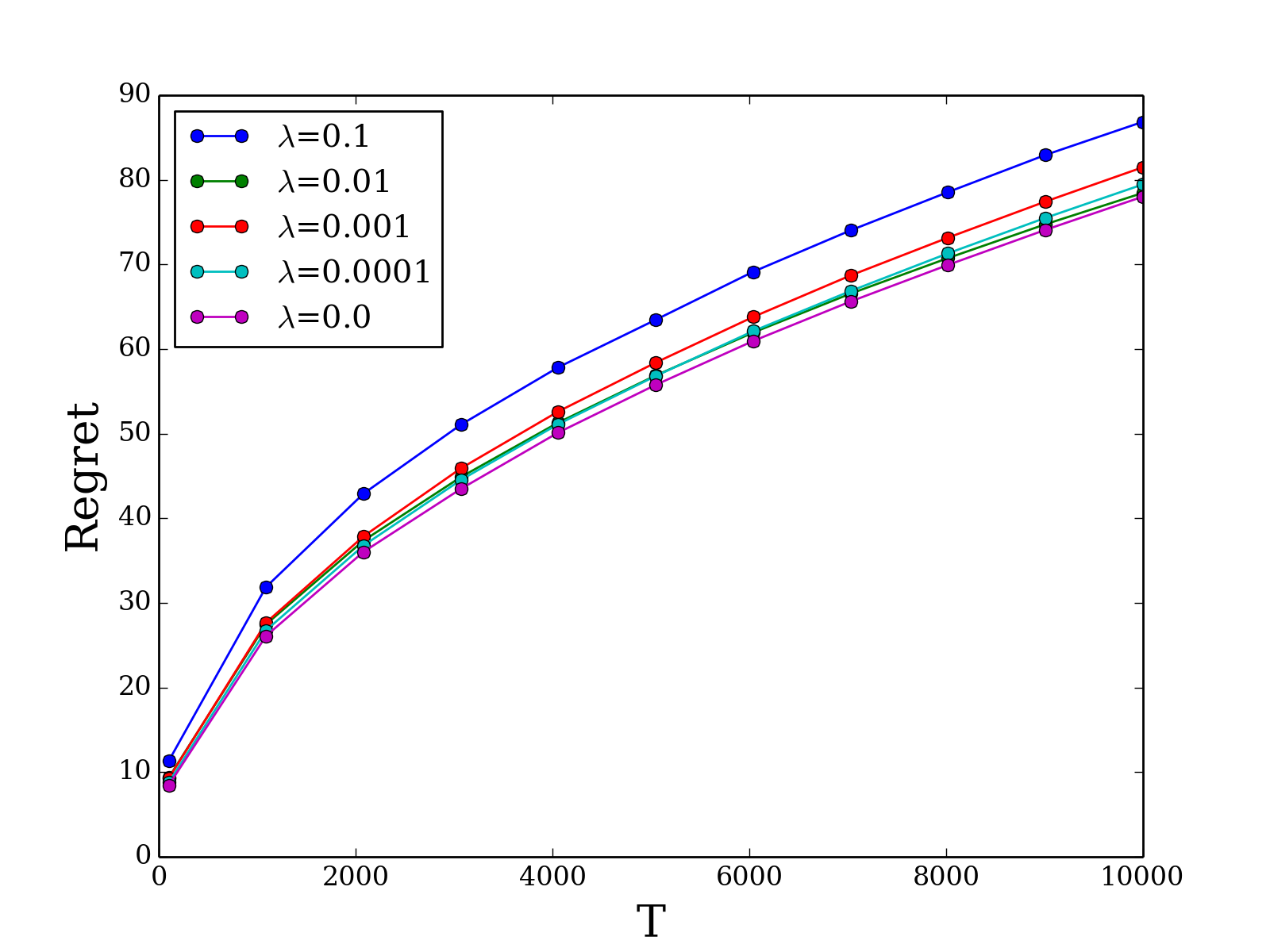
Online allocation problems with resource constraints have a rich history in operations research. In this paper, we introduce the \emph{regularized online allocation problem}, a variant that includes a non-linear regularizer acting on the total resource consumption. In this problem, requests repeatedly arrive over time and, for each request, a decision maker needs to take an action that generates a reward and consumes resources. The objective is to simultaneously maximize additively separable rewards and the value of a non-separable regularizer subject to the resource constraints. Our primary motivation is allowing decision makers to trade off separable objectives such as the economic efficiency of an allocation with ancillary, non-separable objectives such as the fairness or equity of an allocation. We design an algorithm that is simple, fast, and attains good performance with both stochastic i.i.d.~and adversarial inputs. In particular, our algorithm is asymptotically optimal under stochastic i.i.d. input models and attains a fixed competitive ratio that depends on the regularizer when the input is adversarial. Furthermore, the algorithm and analysis do not require convexity or concavity of the reward function and the consumption function, which allows more model flexibility. Numerical experiments confirm the effectiveness of the proposed algorithm and of regularization in an internet advertising application.
翻译:资源限制的在线分配问题在运行研究中有着丰富的历史。 在本文中, 我们引入了 emph{ 正规化的在线分配问题 。 这个变式包括非线性常规化者在资源总消耗量上的行动。 在这个问题中, 请求会反复出现, 对于每项请求, 决策者需要采取行动, 产生奖赏和消耗资源。 目标是在受资源限制的不可分离的常规化器的同时, 尽量扩大累加、 可分离的奖赏和价值。 我们的主要动机是允许决策者交换可分离的目标, 例如与辅助性、 非分离性目标的分配的经济效率, 如分配的公平性或公平性。 我们设计一种简单、 快速的算法, 并且对于每项请求来说, 决策者需要同时采取能产生奖赏和消耗资源的行动。 特别是, 我们的算法在随机性i. i. d. d. 投入模式下, 并获得一个取决于定期化器的固定竞争比率, 当投入是对抗性时, 时取决于定期性分配的经济效率。 此外, 算法和分析法和分析并不要求软性、 性、 和软性 的互联网消费的正规化功能。