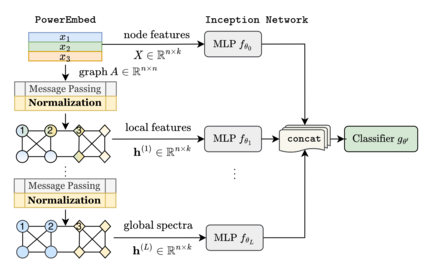
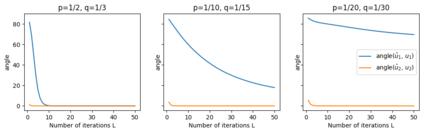
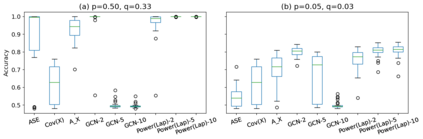
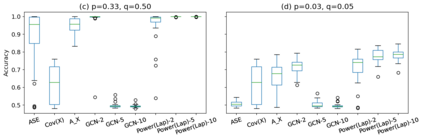
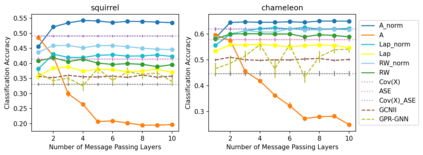
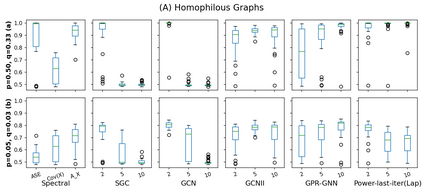
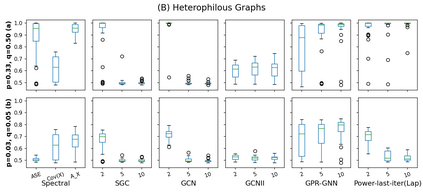
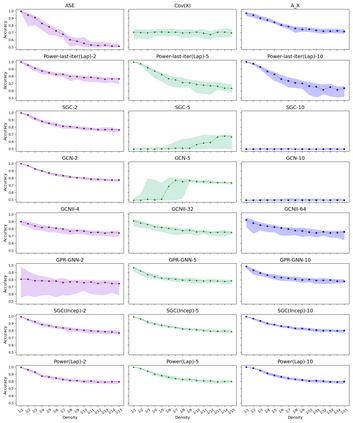
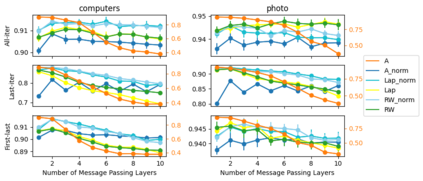
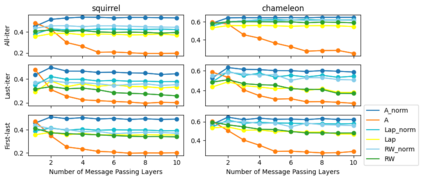
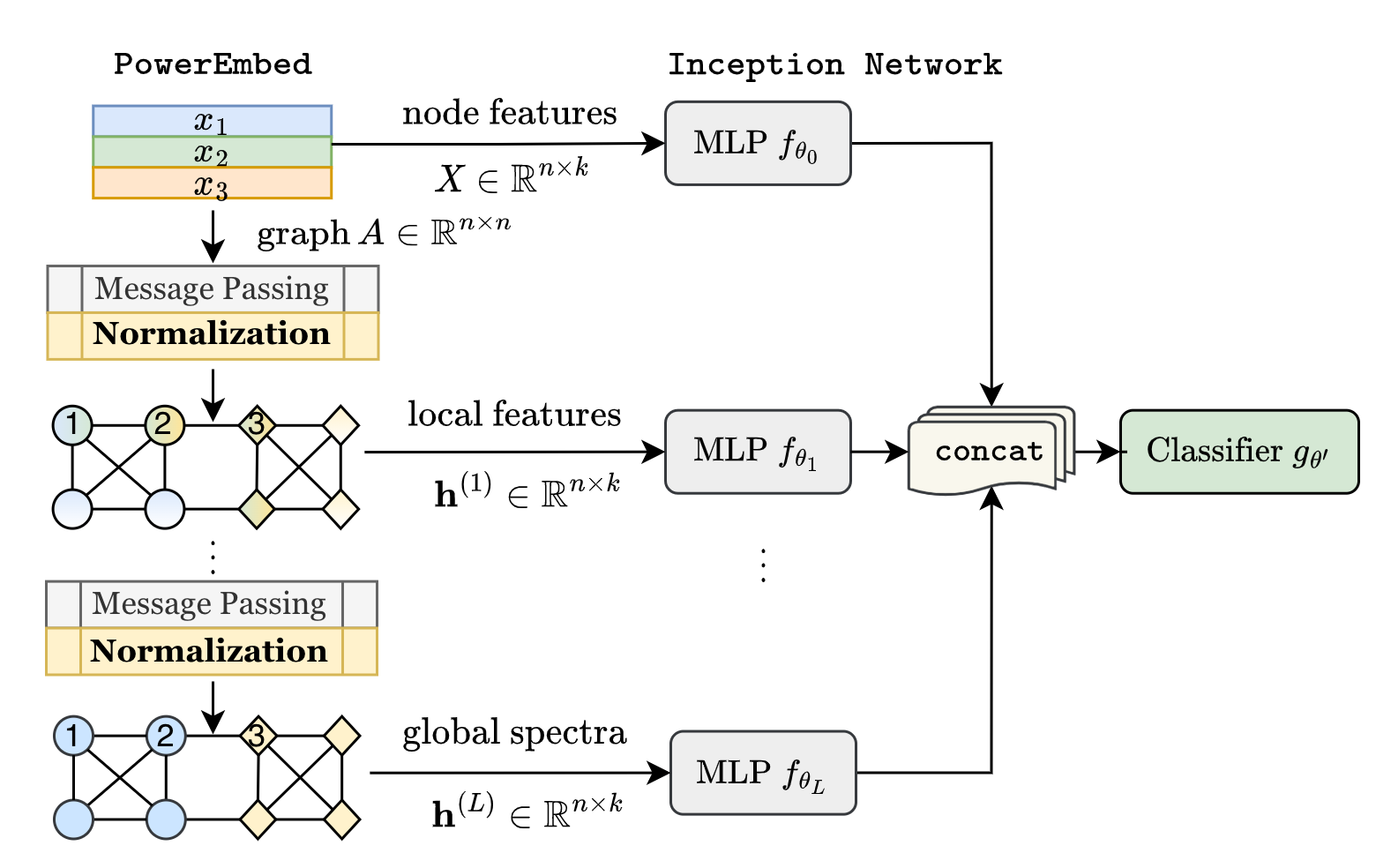
Graph Neural Networks (GNNs) are powerful deep learning methods for Non-Euclidean data. Popular GNNs are message-passing algorithms (MPNNs) that aggregate and combine signals in a local graph neighborhood. However, shallow MPNNs tend to miss long-range signals and perform poorly on some heterophilous graphs, while deep MPNNs can suffer from issues like over-smoothing or over-squashing. To mitigate such issues, existing works typically borrow normalization techniques from training neural networks on Euclidean data or modify the graph structures. Yet these approaches are not well-understood theoretically and could increase the overall computational complexity. In this work, we draw inspirations from spectral graph embedding and propose $\texttt{PowerEmbed}$ -- a simple layer-wise normalization technique to boost MPNNs. We show $\texttt{PowerEmbed}$ can provably express the top-$k$ leading eigenvectors of the graph operator, which prevents over-smoothing and is agnostic to the graph topology; meanwhile, it produces a list of representations ranging from local features to global signals, which avoids over-squashing. We apply $\texttt{PowerEmbed}$ in a wide range of simulated and real graphs and demonstrate its competitive performance, particularly for heterophilous graphs.
翻译:神经网( GNNs) 是非欧元数据极强的深层次学习方法。 普通 GNNs 通常是从Euclidean 数据或修改图形结构的培训神经网中借用正常化技术。 然而, 普通 GNS 是信息传递算法( MPNs), 在本地图形附近集成和合并信号。 然而, 浅的 MPNs 往往错过远程信号, 在某些异性图形上表现不佳, 而深层的MPNNs 可能会受到过度移动或过度对比等问题的影响。 为了缓解这些问题, 现有的工作通常会从Eucliidean 数据或修改图形结构的培训神经网中借用正常化技术。 然而, 这些方法在理论上并不太清楚, 可能会增加总体计算的复杂性。 在这项工作中, 我们从光谱图嵌嵌入的嵌入中提取灵感, 并提议$\ text{ powernameEmbel} -- 一种简单的分层正常化技术来提升MPNs。 我们显示 $ textt{ powembt} poliumextorical extortortortoral exbilts laction laps lactions 。