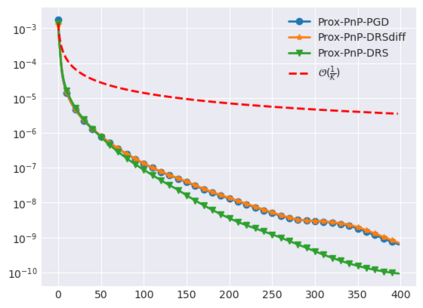
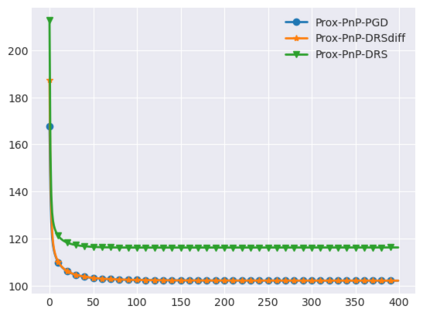
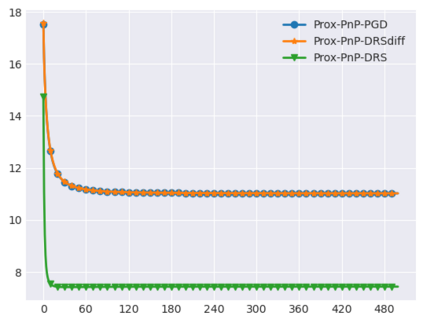
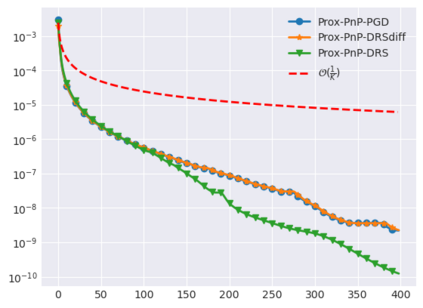
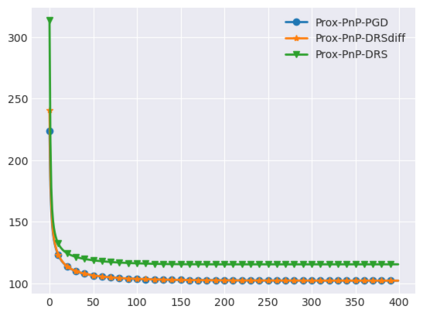
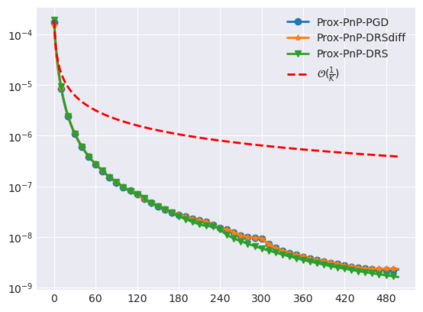
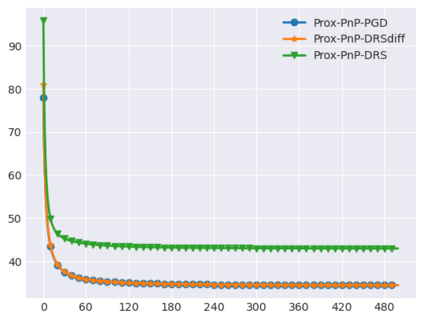
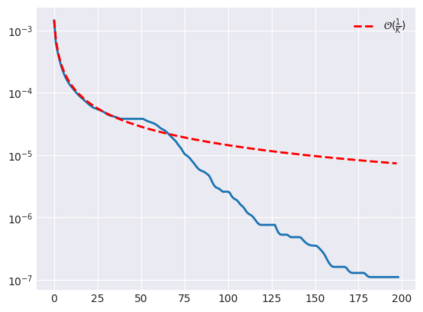
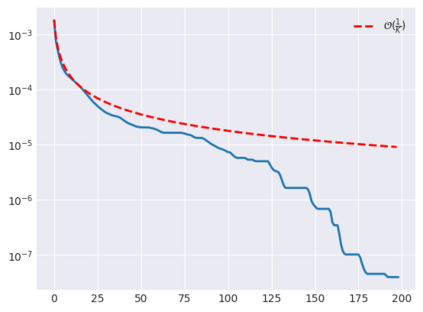
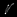Plug-and-Play (PnP) methods solve ill-posed inverse problems through iterative proximal algorithms by replacing a proximal operator by a denoising operation. When applied with deep neural network denoisers, these methods have shown state-of-the-art visual performance for image restoration problems. However, their theoretical convergence analysis is still incomplete. Most of the existing convergence results consider nonexpansive denoisers, which is non-realistic, or limit their analysis to strongly convex data-fidelity terms in the inverse problem to solve. Recently, it was proposed to train the denoiser as a gradient descent step on a functional parameterized by a deep neural network. Using such a denoiser guarantees the convergence of the PnP version of the Half-Quadratic-Splitting (PnP-HQS) iterative algorithm. In this paper, we show that this gradient denoiser can actually correspond to the proximal operator of another scalar function. Given this new result, we exploit the convergence theory of proximal algorithms in the nonconvex setting to obtain convergence results for PnP-PGD (Proximal Gradient Descent) and PnP-ADMM (Alternating Direction Method of Multipliers). When built on top of a smooth gradient denoiser, we show that PnP-PGD and PnP-ADMM are convergent and target stationary points of an explicit functional. These convergence results are confirmed with numerical experiments on deblurring, super-resolution and inpainting.
翻译:PnP (PnP) 方法解决了错误的反向问题, 通过迭代正统算法解决了错误的反向问题, 代之以一个淡化操作取代一个准分子操作员。 当应用于一个深神经网络的隐隐性器时, 这些方法已经显示了图像恢复问题的最先进的视觉性能。 但是, 它们的理论趋同分析仍然不完整。 大多数现有的趋同结果都考虑的是非蒸发的隐性算法, 这是一种不现实的, 或将其分析限制在要解决的逆向问题中强烈的 convex 数据趋同性术语中。 最近, 提议用一个深神经网络的功能参数来将脱色化器作为渐渐渐渐的功能性下降步骤。 使用这种脱色器可以保证半夸度- Split( PnP-HQS) 版本的 PnPn- Prbl) 迭接合算法。 我们的渐渐渐变调调调调调调调调调调调调调调调调调调调调调调调调调调调调调调调调调调调调调调调调调调调调调调调调。